练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆的左、右两个焦点分别为，离心率，短轴长为2.

    （1）求椭圆的方程；

    （2）点为椭圆上的一动点（非长轴端点），的延长线与椭圆交于点， 的延长线与椭圆交于点，求面积的最大值.

    【答案】（1）椭圆的标准方程为 （2）面积的最大值为

    【解析】试题分析：（1） 由题意得，再由， 标准方程为；（2）①当的斜率不存在时，不妨取

    ； ②当的斜率存在时，设的方程为，联立方程组

    ，又直线的距离 点到直线的距离为 面积的最大值为.

    试题解析：（1） 由题意得，解得，

    ∵，∴， ，

    故椭圆的标准方程为

    （2）①当直线的斜率不存在时，不妨取

    ，

    故；

    ②当直线的斜率存在时，设直线的方程为 ，

    联立方程组，

    化简得，

    设

    点到直线的距离

    因为是线段的中点，所以点到直线的距离为，

    ∴

    综上， 面积的最大值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知等边三角形的边长为，为边的中点，沿将折成直二面角，则三棱锥的外接球的表面积为_____

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列五个命题：

    ①已知直线、和平面，若，，则；

    ②平面上到一个定点和一条定直线的距离相等的点的轨迹是一条抛物线；

    ③双曲线，则直线与双曲线有且只有一个公共点；

    ④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直；

    ⑤过的直线与椭圆交于、两点，线段中点为，设直线斜率为，直线的斜率为，则等于.

    其中，正确命题的序号为_______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了研究某学科成绩是否与学生性别有关，采用分层抽样的方法，从高三年级抽取了30名男生和20名女生的该学科成绩，得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图，规定80分以上为优分（含80分）．

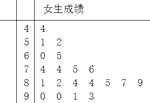
    （Ⅰ）（i）请根据图示，将2×2列联表补充完整；


    优分

    非优分

    总计

    男生




    女生




    总计



    50

    （ii）据此列联表判断，能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”？

    （Ⅱ）将频率视作概率，从高三年级该学科成绩中任意抽取3名学生的成绩，求至少2名学生的成绩为优分的概率．

    附：


    0.100

    0.050

    0.010

    0.001


    2.706

    3.841

    6.635

    10.828

    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】科技创新能力是决定综合国力和国际竞争力的关键因素，也是推动经济实现高质量发展的重要支撑，而研发投入是科技创新的基本保障，下图是某公司从2010年到2019年这10年研发投入的数据分布图:

    其中折线图是该公司研发投入占当年总营收的百分比，条形图是当年研发投入的数值(单位:十亿元).

    (I)从2010年至2019年中随机选取一年，求该年研发投入占当年总营收的百分比超过10%的概率；

    (II)从2010年至2019年中随机选取两个年份，设X表示其中研发投入超过500亿元的年份的个数，求X的分布列和数学期望；

    (III)根据图中的信息，结合统计学知识，判断该公司在发展的过程中是否比较重视研发，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近五年来某草场羊只数量与草场植被指数两变量间的关系如表所示，绘制相应的散点图，如图所示：

    年份

    1

    2

    3

    4

    5

    羊只数量（万只）

    1.4

    0.9

    0.75

    0.6

    0.3

    草地植被指数

    1.1

    4.3

    15.6

    31.3

    49.7

    根据表及图得到以下判断：①羊只数量与草场植被指数成减函数关系；②若利用这五组数据得到的两变量间的相关系数为，去掉第一年数据后得到的相关系数为，则；③可以利用回归直线方程，准确地得到当羊只数量为2万只时的草场植被指数；以上判断中正确的个数是（ ）

    A.0B.1C.2D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（a∈R且a≠0）.

    （1）当a时，求曲线y＝f（x）在点（1，f（1））处的切线方程；

    （2）讨论函数f（x）的单调性与单调区间；

    （3）若y＝f（x）有两个极值点x1，x2，证明：f（x1）+f（x2）＜9﹣lna.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年春节期间，新型冠状病毒（2019﹣nCoV）疫情牵动每一个中国人的心，危难时刻全国人民众志成城．共克时艰，为疫区助力．我国S省Q市共100家商家及个人为缓解湖北省抗疫消毒物资压力，募捐价值百万的物资对口输送湖北省H市．

    （1）现对100家商家抽取5家，其中2家来自A地，3家来自B地，从选中的这5家中，选出3家进行调研．求选出3家中1家来自A地，2家来自B地的概率．

    （2）该市一商家考虑增加先进生产技术投入，该商家欲预测先进生产技术投入为49千元的月产增量．现用以往的先进技术投入xi（千元）与月产增量yi（千件）（i＝1，2，3，…，8）的数据绘制散点图，由散点图的样本点分布，可以认为样本点集中在曲线的附近，且：，，，，，其中，，，根据所给的统计量，求y关于x回归方程，并预测先进生产技术投入为49千元时的月产增量．

    附：对于一组数据（u1，v1）（u2，v2），其回归直线v＝α+βu的斜率和截距的最小二乘法估计分别为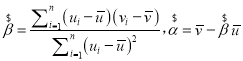

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1为某省2018年1~4月快递业务量统计图，图2是该省2018年1~4月快递业务收入统计图，下列对统计图理解错误的是（ ）

    A. 2018年1~4月的业务量，3月最高，2月最低，差值接近2000万件

    B. 2018年1~4月的业务量同比增长率均超过50%，在3月底最高

    C. 从两图来看，2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致

    D. 从1~4月来看，该省在2018年快递业务收入同比增长率逐月增长

    查看答案和解析>>

    同步练习册答案