
【题目】已知函数![]() ,
,![]()
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)是否存在实数![]() 使得
使得![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)由函数的解析式可得 1﹣![]() >0,即
>0,即 ![]() >0,由此求得定义域,定义域关于原点对称,且f(﹣x)+f(x)=0,可得f(x)是奇函数.
>0,由此求得定义域,定义域关于原点对称,且f(﹣x)+f(x)=0,可得f(x)是奇函数.
(2)a>1时,根据函数f(x)在[m,n]上是增函数,可得函数的值域不可能为[1+logan,1+logam],此时,a不存在.
0<a<1时,f(x)单调递减,则由![]() =1+logax,可得ax2+(2a﹣1)x+2=0.由题意可得,ax2+(2a﹣1)x+2=0有两个大于2的不等实根.根据二次函数的性质求得a的范围.
=1+logax,可得ax2+(2a﹣1)x+2=0.由题意可得,ax2+(2a﹣1)x+2=0有两个大于2的不等实根.根据二次函数的性质求得a的范围.
(1)定义域为{x|x<-2或x>2}, 且![]() ,所以f(x)是奇函数.
,所以f(x)是奇函数.
(2)a>1时,根据函数f(x)在[m,n]上是增函数,1+logan>1+logam,可得函数的值域不可能为[1+logan,1+logam],此时,a不存在.
0<a<1时,f(x)单调递减,则![]() =
=![]()
![]()
![]()
即![]() 有两个大于2的不等实根,
有两个大于2的不等实根,
设g(x)= ![]() ,则
,则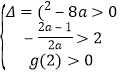 , 解得
, 解得![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设双曲线C的中心为点O,若有且只有一对相交于点O,所成的角为60°的直线A1B1和A2B2,使| A1B1|=| A2B2|,其中A1,B1和A2,B2分别是这对直线与双曲线C的交点,则该双曲线的离心率的取值范围是( )
A. (![]() ,2] B. [
,2] B. [![]() ,2) C. (
,2) C. (![]() ,+
,+![]() ) D. [
) D. [![]() ,+
,+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点
的一个焦点![]() 与抛物线
与抛物线![]() 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为![]() .
.
(1)求该椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰为弦
恰为弦![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据条件,求下列曲线的方程.
(1)已知两定点![]() ,曲线上的点
,曲线上的点![]() 到
到![]() 距离之差的绝对值为
距离之差的绝对值为![]() ,求曲线的方程;
,求曲线的方程;
(2)在 ![]() 轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为
轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为![]() 的椭圆的标准方程.
的椭圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明一家订阅的晚报会在下午5:30~6:30之间的任何一个时间随机地被送到,小明一家人在下午6:00~7:00之间的任何一个时间随机地开始晚餐.
(1)你认为晚报在晚餐开始之前被送到和晚餐开始之后被送到哪一种可能性更大?
(2)晚报在晚餐开始之前被送到的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|y=f(x)},若对于任意实数对(x1,y1)∈M,存在(x2,y2)∈M,使x1x2+y1y2=0成立,则称集合M具有∟性,给出下列四个集合:
①M={(x,y)|y=x3﹣2x2+3}; ②M={(x,y)|y=log2(2﹣x)};
③M={(x,y)|y=2﹣2x}; ④M={(x,y)|y=1﹣sinx};
其中具有∟性的集合的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com