练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求下列函数的导函数：
    ①f（x）=x3+log2x；
    ②f（x）=
    cosx
    ex
    ．
    考点：导数的运算
    专题：导数的概念及应用
    分析：根据函数的导数公式直接进行求解即可得到结论．
    解答： 解：①∵f（x）=x3+log2x；
    ∴f′（x）=3x2+
    1
    xln2
    ；
    ②∵f（x）=
    cosx
    ex
    ，
    ∴f′（x）=
    (cosx)′•ex-cosx•(ex)′
    (ex)2
    =
    -sinx-cosx
    ex
    ．
    点评：本题主要考查导数的计算，要求熟练掌握常见函数的导数公式以及导数的运算法则，比较基础．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设函数f（x）=-
    a
    2
    x2+（a+1）x-lnx（a∈R）．
    （1）当a=0时，求函数f（x）的极值；
    （2）当a＞0时，讨论函数f（x）的单调性；
    （3）若对任意a∈（2，3）及任意x1，x2∈[1，2]，恒有
    a2-1
    2
    m+ln2＞|f（x1）-f（x2）|成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一个农技站为了考察某种麦穗长的分布情况，在一块试验地里抽取了100个麦穗，量得长度如下（单位：cm）：
    6.5　6.4　6.7　5.8　5.9　5.9　5.2　4.0　5.4　4.6
    5.8　5.5　6.0　6.5　5.1　6.5　5.3　5.9　5.5　5.8
    6.2　5.4　5.0　5.0　6.8　6.0　5.0　5.7　6.0　5.5
    6.8　6.0　6.3　5.5　5.0　6.3　5.2　6.0　7.0　6.4
    6.4　5.8　5.9　5.7　6.8　6.6　6.0　6.4　5.7　7.4
    6.0　5.4　6.5　6.0　6.8　5.8　6.3　6.0　6.3　5.6
    5.3　6.4　5.7　6.7　6.2　5.6　6.0　6.7　6.7　6.0
    5.6　6.2　6.1　5.3　6.2　6.8　6.6　4.7　5.7　5.7
    5.8　5.3　7.0　6.0　6.0　5.9　5.4　6.0　5.2　6.0
    6.3　5.7　6.8　6.1　4.5　5.6　6.3　6.0　5.8　6.3
    根据上面的数据列出频率分布表、绘出频率分布直方图，并估计长度在5.75～6.05cm之间的麦穗在这批麦穗中所占的百分比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    a
    =（cos
    3
    2
    x，sin
    3
    2
    x），
    b
    =（cos
    x
    2
    ，-sin
    x
    2
    ），且x∈[0，
    π
    2
    ]，
    （1）求
    a
    •
    b
    及|
    a
    +
    b
    |；
    （2）求函数f（x）=
    a
    •
    b
    -2|
    a
    +
    b
    |的最小值；
    （3）若f（x）=
    a
    •
    b
    -λ|
    a
    +
    b
    |的最小值是-
    3
    2
    ，求实数λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=sin（2x+
    π
    6
    ）+sin（2x-
    π
    6
    ）+2cos2x，（x∈R）
    （1）求函数f（x）的单调递减区间；    
    （2）求使f（x）≥2的x的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求函数y=
    x2
    x+3
    在x=2处的切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

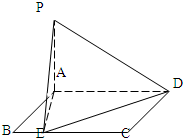    如图，四边形ABCD为矩形，且AD=4，AB=2，PA=1，PA⊥平面ABCD，E为线段BC上的动点．
    （1）当E为线段BC的中点时，求证：DE⊥平面PAE；
    （2）若BE=1，求二面角P-ED-A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=lnx-
    1
    2
    ax2-2x+1，a∈R
    （Ⅰ）若f（x）在x=2处的切线与直线2x+y=0垂直，求a的值；
    （Ⅱ）若f（x）存在单调递减区间，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数y=-2cosx，x∈[0，2π]的图象和直线y=-2围成的一个封闭的平面图形的面积是
     
    ．

    查看答案和解析>>

    同步练习册答案