
分析 (1)利用f(0)=0,即可求a的值;
(2)当0≤x≤1时,关于x的方程f(x)+1=t有解,求出函数的值域,即可求实数t的取值范围;
(3)利用函数的单调性,化不等式为具体不等式,分类讨论,即可解关于x的不等式f(x2-mx)≥f(2x-2m).
解答 解:(1)∵x∈R,∴f(0)=0,∴a=-1….(3分)
(2)∵$f(x)=\frac{2}{{{3^x}+1}}-1∴f(x)+1=\frac{2}{{{3^x}+1}}$,∵0≤x≤1,∴2≤3x+1≤4….(5分)
∴$\frac{1}{2}≤f(x)+1≤1$….(7分)∴$\frac{1}{2}≤t≤1$….(8分)
(3)$f(x)=\frac{2}{{{3^x}+1}}-1$在R上单调递减,….(9分)
f(x2-mx)≥f(2x-2m)x2-mx≤2x-2m….(10分)
x2-(m+2)x+2m≤0(x-2)(x-m)≤0….(11分)
①当m>2时,不等式的解集是{x|2≤x≤m}
②当m=2时,不等式的解集是{x|x=2}
③当m<2时,不等式的解集是{x|m≤x≤2}….(14分)
点评 本题考查奇函数的性质,考查函数的值域,考查学生解不等式的能力,正确转化是关键.


科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
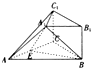 用如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.
用如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x≠0,则x+$\frac{1}{x}$≥2 | |
| B. | 若直线x-ay=0与直线x-ay=0互相垂直,则a=1 | |
| C. | 命题:“若x2=1,则x=1或x=-1”的逆否命题为:“若x≠1,且x≠-1,则x2≠1” | |
| D. | 一个命题的否命题为真,则它的逆否命题一定为真 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com