练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．学校举办了一次田径运动会，某班有8人参赛，后有举办了一次球类运动会，这个班有12人参赛，两次运动会都参赛的有3人，两次运动会中，这个班共有多少名同学参赛？（　　）
    A．17B．18C．19D．20

    分析 设A为田径运动会参赛的学生的集合，B为球类运动会参赛的学生的集合，那么A∩B就是两次运动会都参赛的学生的集合，card（A），card（B），card（A∩B）是已知的，于是可以根据上面的公式求出card（A∪B）．

    解答 解：设A={x|x是参加田径运动会比赛的学生}，B={x|x是参加球类运动会比赛的学生}，
    A∩B={x|x是两次运动会都参加比赛的学生}，
    A∪B={x|x是参加所有比赛的学生}．
    因此card（A∪B）=card（A）+card（B）-card（A∩B）=8+12-3=17．
    故两次运动会中，这个班共有17名同学参赛．
    故选：A

    点评 本题考查集合中元素个数的求法，是中档题，解题时要认真审题，注意公式card（A∪B）=card（A）+card（B）-card（A∩B）的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    6．设复数z满足z（1+i）=|$\sqrt{3}$-i|（i是虚数单位），则复数z在复平面内对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

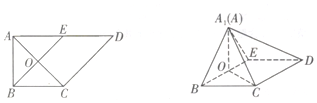    7．如图甲，在直角梯形ABCD中，AD∥BC，∠BAD=$\frac{π}{2}$，AD=2，AB=BC=1，E是AD的中点，O是AC与BE的交点，将△ABE沿BE折起到△A1BE的位置，如图乙
    （1）证明：CD⊥平面A1OC
    （2）若平面A1BE⊥平面BCDE，求点B与平面A1CD的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．F1、F2是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两焦点，Q是椭圆上任一点，过一焦点引∠F1QF2的外角平分线的垂线，则垂足M的轨迹为（　　）
    A．圆B．椭圆C．双曲线D．抛物线

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．设a，b∈R，则“a+b＞4”是“a＞2且b＞2”的必要不充分条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数$f（x）=\frac{2}{{{3^x}+1}}+a（a∈R）$为奇函数，
    （1）求a的值；
    （2）当0≤x≤1时，关于x的方程f（x）+1=t有解，求实数t的取值范围；
    （3）解关于x的不等式f（x2-mx）≥f（2x-2m）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．如图，在菱形ABCD中，AB=2，∠ABC=60°，BD∩AC=O，现将其沿菱形对角线BD折起得空间四边形EBCD，使EC=$\sqrt{2}$．
    （Ⅰ）求证：EO⊥CD．
    （Ⅱ）求点O到平面EDC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知直线2x+y-2=0与直线4x+my+6=0平行，则它们之间的距离为$\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知偶函数f（x）在（0，+∞）上递减，已知a=0.2${\;}^{\sqrt{2}}$，b=log${\;}_{\sqrt{2}}$0.2，c=$\sqrt{2}$0.2，则f（a），f（b），f（c）  大小为（　　）
    A．f（a）＞f（b）＞f（c）B．f（a）＞f（c）＞f（b）C．f（b）＞f（a）＞f（c）D．f（c）＞f（a）＞f（b）

    查看答案和解析>>

    同步练习册答案