
分析 (1)分类讨论,求出△MON(O为坐标原点)面积的最小值,即可求抛物线C的方程;
(2)分类讨论,利用直线l上的点Q满足$\frac{2}{{|FQ{|^2}}}=\frac{1}{{|FM{|^2}}}+\frac{1}{{|FN{|^2}}}$,求出弦长,即可求点Q的轨迹方程.
解答 解:(1)①当l⊥x时,l:x=1,${y_M}=\sqrt{2p}$,${S_△}=\frac{1}{2}×2\sqrt{2p}×1=\sqrt{2p}=2,p=2$
②当l斜率存在时,设l:y=k(x-1)与y2=2px联立,得k2x2-(2k2+2p)+k2=0,${S_△}=\frac{1}{2}×2\sqrt{2p+\frac{{4{p^2}}}{k^2}}>\sqrt{2p}$,所以当l⊥x时面积最小,
所以p=2,抛物线方程为y2=4x…(6分)
(2)设Q(x,y),M(x1,y1),N(x2,y2),
①当l⊥x时,l:x=1,y1=2,y2=-2,点Q(1,±2)
②当l斜率存在时,设l:y=k(x-1)与y2=4x联立,得k2x2-(2k2+4)+k2=0,
|FQ|2=(1+k2)(x-1)2,$|FM{|^2}=(1+{k^2}){({x_1}-1)^2}$,$|FN{|^2}=(1+{k^2}){({x_2}-1)^2}$,
由$\frac{2}{{|FQ{|^2}}}=\frac{1}{{|FM{|^2}}}+\frac{1}{{|FN{|^2}}}$得$\frac{2}{{{{(x-1)}^2}}}=\frac{1}{{{{({x_1}-1)}^2}}}+\frac{1}{{{{({x_2}-1)}^2}}}=\frac{{{{({x_1}-1)}^2}+{{({x_2}-1)}^2}}}{{{{({x_1}-1)}^2}{{({x_2}-1)}^2}}}$=$\frac{k^2}{2}+1$,
因为$k=\frac{y}{x-1}$,所以$\frac{2}{{{{(x-1)}^2}}}=\frac{y^2}{{2{{(x-1)}^2}}}+1(x≠1)$,
化简得2(x-1)2+y2=4(x≠±1),Q(1,±2)也符合.
所以点Q的轨迹方程为2(x-1)2+y2=4…(6分)
点评 本题考查轨迹方程,考查抛物线方程,考查直线与抛物线的位置关系,属于中档题.


科目:高中数学 来源: 题型:解答题
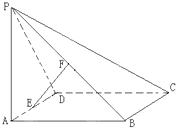 如图:四棱锥P-ABCD的底面是平行四边形,∠DAB=60°,平面PAB⊥ABD,
如图:四棱锥P-ABCD的底面是平行四边形,∠DAB=60°,平面PAB⊥ABD,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,-1) | C. | (-$\frac{1}{16}$,0) | D. | (0,-$\frac{1}{16}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 数学成绩好 | 数学成绩一般 | 总计 | |
| 物理成绩好 | |||
| 物理成绩一般 | |||
| 总计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $3\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 2$\sqrt{2}$+1 | D. | $\frac{{3\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 生二胎 | 不生二胎 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com