
分析 分别以BC、BA所在直线为x轴和y轴建立平面直角坐标系,设出O的坐标,由向量共线求出O的坐标,得到$\overrightarrow{AO}$的坐标,然后由向量数量积求得答案.
解答 解:如图,
分别以BC、BA所在直线为x轴和y轴建立平面直角坐标系,
则B(0,0),C(4,0),A(0,3),
设O(m,m),
设$\overrightarrow{AO}$方向上的单位向量为$\overrightarrow{e}$,
则$\overrightarrow{e}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AC}=\frac{1}{3}(0,-3)+\frac{1}{5}(4,3)$=($\frac{4}{5},-\frac{8}{5}$),
又$\overrightarrow{AO}=(m,m-3)$,∴$\frac{m-3}{m}=-2$,即m=1.
∴$\overrightarrow{AO}=(1,-2)$,
∴$\overrightarrow{AO}•\overrightarrow{BC}$=(1,-2)•(4,0)=4.
故答案为:4.
点评 本题考查向量知识,考查平面向量基本定理的运用,考查学生的计算能力,关键是运用坐标运用算求解,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
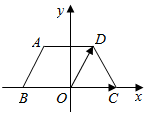 如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.
如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx在第三象限内是增函数 | B. | 函数y=sinx(x∈R)的值域是(-1,1) | ||
| C. | y=cosx在x=2kπ(k∈Z)时取值最大 | D. | y=tanx在整个定义域内都是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (0,4) | C. | ($\frac{1}{4}$,4) | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∉R,x2≠x | B. | ?x∈R,x2=x | C. | ?x0∈R,x${\;}_{0}^{2}$≠x0 | D. | ?x0∈R,x${\;}_{0}^{2}$=x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{3}{5}$i | C. | -$\frac{3}{5}$ | D. | -$\frac{3}{5}$i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com