
分析 (1)由题意可得0<x<1时,g′(x)=2x+2+$\frac{a}{x}$>0恒成立,即a>-2x2-2x=-2${(x+\frac{1}{2})}^{2}$+$\frac{1}{2}$,求得2${(x+\frac{1}{2})}^{2}$+$\frac{1}{2}$ 的最大值,可得a的范围.
(2)利用导数研究函数的单调性以极值,再根据极值的符号确定函数的零点符号.
解答 解:(1)∵函数f(x)=x2-2,函数g(x)=f(x)+2(x+1)+alnx在区间(0,1)上单调,
∴0<x<1时,g′(x)=2x+2+$\frac{a}{x}$>0恒成立,即a>-2x2-2x=-2${(x+\frac{1}{2})}^{2}$+$\frac{1}{2}$,
而m(x)=-2${(x+\frac{1}{2})}^{2}$+$\frac{1}{2}$ 在区间(0,1)上单调递减,∴-2${(x+\frac{1}{2})}^{2}$+$\frac{1}{2}$<m(0)=0,∴a≥0.
(2)∵函数$h(x)=ln(1+{x^2})-\frac{1}{2}f(x)-k$=ln(1+x2)-$\frac{1}{2}$(x2-2)-k=ln(1+x2)-$\frac{1}{2}$x2+1-k 的定义域为R,
h′(x)=$\frac{2x}{1{+x}^{2}}$-x-0=$\frac{x(1{-x}^{2})}{1{+x}^{2}}$,令h′(x)=0,求得x=0,或x=1 或x=-1,
列表:
| x | (-∞,-1 ) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,+∞) |
| f′(x)的符号 | + | - | + | - | |||
| f(x) | 增 | 极大值 ln2+$\frac{1}{2}$-k | 减 | 极小值 1-k | 增 | 极大值 ln2+$\frac{1}{2}$-k | 减 |
点评 本题主要考查函数的零点,函数的单调性与导数的关系,利用导数求函数的最值,属于难题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
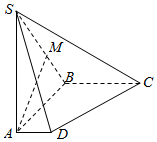 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA丄底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1.M是棱SB的中点.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,侧棱SA丄底面ABCD,AB垂直于AD和BC,SA=AB=BC=2,AD=1.M是棱SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1008 | B. | -1008 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
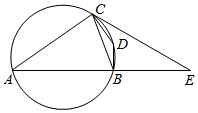 如图,四边形ABDC内接于圆,BD=CD,BD⊥AB,过点C的圆的切线与AB的延长线交于点E,BC=BE,AE=2,则AB=$\sqrt{5}$-1.
如图,四边形ABDC内接于圆,BD=CD,BD⊥AB,过点C的圆的切线与AB的延长线交于点E,BC=BE,AE=2,则AB=$\sqrt{5}$-1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com