
| A. | $\frac{15}{2}$ | B. | $\frac{29}{4}$ | C. | 7 | D. | $\frac{27}{4}$ |
分析 设AC斜率为k1,BC斜率为k2,推出直线AC、直线BC的方程,求出△ABC的面积S的表达式,求出面积的最大值即可.
解答 解:设AC斜率为k1,BC斜率为k2,则
直线AC的方程为y=k1x+t,直线BC的方程为y=k2x+t+6;
由方程组$\left\{\begin{array}{l}{y{=k}_{1}x+t}\\{y{=k}_{2}x+t+6}\end{array}\right.$,得C点的横坐标为xc=$\frac{6}{{k}_{1}{-k}_{2}}$,
∵|AB|=t+6-t=6,
∴S△ABC=$\frac{1}{2}$•$\frac{6}{{k}_{1}{-k}_{2}}$•6=$\frac{18}{{k}_{1}{-k}_{2}}$,
由于圆M与AC相切,所以$\frac{{|k}_{1}+t|}{\sqrt{1{{+k}_{1}}^{2}}}$=1,∴k1=$\frac{1{-t}^{2}}{2t}$;
同理,k2=$\frac{1{-(t+6)}^{2}}{2(t+6)}$,
∴k1-k2=$\frac{3{(t}^{2}+6t+1)}{{t}^{2}+6t}$,
∴S△ABC=$\frac{6{(t}^{2}+6t)}{{t}^{2}+6t+1}$=6(1-$\frac{1}{{t}^{2}+6t+1}$),
∵-5≤t≤-2,∴-2≤t+3≤1,∴-8≤t2+6t+1≤-4,
∴S△ABC的最大值为6×(1+$\frac{1}{4}$)=$\frac{15}{2}$.
故选:A.
点评 本题考查了直线与圆的位置关系,三角形面积的最值问题,也考查计算能力的应用问题,是综合性题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
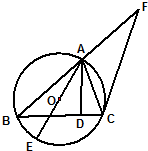 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆台是直角梯形绕其一边旋转而成的旋转体 | |
| B. | 棱台的上下底面一定相似,但侧棱长不一定相等 | |
| C. | 顶点在底面的投影为底面中心的棱锥为正三棱锥 | |
| D. | 圆锥是直角三角形绕其一边旋转而成的旋转体 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | D⊆A | B. | D=B | C. | D⊆C | D. | D=C |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
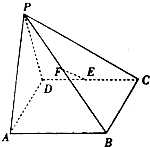 在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,侧面PAD为等边三角形且平面PAD⊥底面ABCD,E、F分别为CD、PB的中点.
在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,侧面PAD为等边三角形且平面PAD⊥底面ABCD,E、F分别为CD、PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com