【题目】经测算，某型号汽车在匀速行驶过程中每小时耗油量
(升)与速度
(千米／每小时) 
的关系可近似表示为：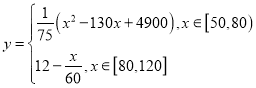
.
（Ⅰ）该型号汽车速度为多少时，可使得每小时耗油量最低？
（Ⅱ）已知
两地相距120公里，假定该型号汽车匀速从
地驶向
地，则汽车速度为多少时总耗油量最少？
培优好卷单元加期末卷系列答案科目：高中数学 来源： 题型：
【题目】某商场销售某件商品的经验表明，该商品每日的销量
（单位：千克）与销售价格
（单位：元/千克）满足关系式
，其中
，
为常数。已知销售价格为5元/千克时，每日可售出该商品11千克。
（Ⅰ）求实数
的值；
（Ⅱ）若该商品的成本为3元/千克，试确定销售价格
的值，使商场每日销售该商品所获得的利润最大。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下面几种推理是合情推理的是 （ ）
①由圆的性质类比出球的有关性质
②由直角三角形、等腰三角形、等边三角形内角和是180°归纳出所有三角形的内角和都是180°
③某次考试张军成绩是100分，由此推出全班同学成绩都是100分
④数列1，0，1，0，…，推测出每项公式
A. ①② B. ①③④ C. ①②④ D. ②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（Ⅰ）若函数
在
处取得极值，求实数
的值；
（Ⅱ）在(Ⅰ)的条件下，函数
(其中
为函数的导数)的图像关于直线
对称，求函数
单调区间；
（Ⅲ）在(Ⅱ)的条件下，若对任意的
，都有
恒成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下面是某市环保局连续30天对空气质量指数的监测数据:
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
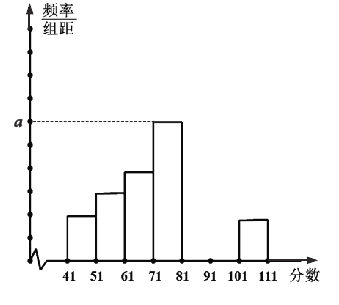
（Ⅰ）完成下面的频率分布表；
（Ⅱ）完成下面的频率分布直方图，并写出频率分布直方图中
的值；
（Ⅲ）在本月空气质量指数大于等于91的这些天中随机选取两天，求这两天中至少有一天空气质量指数在区间
内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若数列
满足
（
； 
， 
），称数列
为
数列，记
为其前
项和.
（Ⅰ）写出一个满足
，且
的
数列
；
（Ⅱ）若
， 
，证明：若
数列
是递增数列，则
；反之，若
，则
数列
是递增数列；
（Ⅲ）对任意给定的整数
（
），是否存在首项为0的
数列
，使得
？如果存在，写出一个满足条件的
数列
；如果不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（1）求
的展开式中
的系数及展开式中各项系数之和；
（2）从0，2，3，4，5，6这6个数字中任取4个组成一个无重复数字的四位数，求满足条件的四位数的个数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛.为了了解这次竞赛的成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计，请你根据尚未完成的频率分布表和频率分布直方图，回答下面问题：
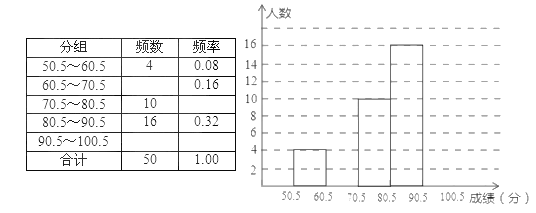
（1）结合图表信息，补全频率分布直方图；
（2）对于参加这次竞赛的900名学生，估计成绩不低于76分的约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
