
【题目】下面是某市环保局连续30天对空气质量指数的监测数据:
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
(Ⅰ)完成下面的频率分布表;
(Ⅱ)完成下面的频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;
(Ⅲ)在本月空气质量指数大于等于91的这些天中随机选取两天,求这两天中至少有一天空气质量指数在区间![]() 内的概率.
内的概率.

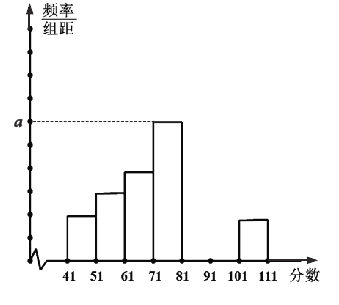
【答案】(Ⅰ)答案见解析;(Ⅱ)答案见解析;(Ⅲ)0.7.
【解析】试题分析:
(1)由题意计算相应的频数和频率即可补全频率分布表;
(2)完成频率分布直方图,结合区间![]() 的频率为
的频率为![]() ,可得
,可得![]() ;
;
(3)由题意列出所有可能的事件,然后结合题意和古典概型的计算公式可得这两天中至少有一天空气质量指数在区间![]() 内的概率是0.7.
内的概率是0.7.
试题解析:
(Ⅰ)如下图所示
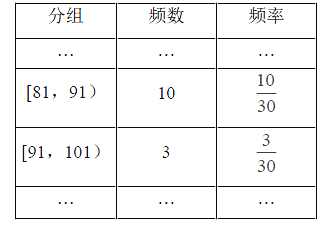
(Ⅱ)如下图所示
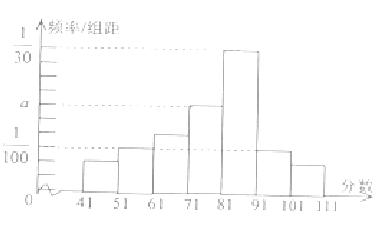
由已知,空气质量指数在区间![]() 的频率为
的频率为![]() ,所以
,所以![]()
(Ⅲ)设![]() 表示事件“在本月空气质量指数大于等于91的这些天中随机选取两天,这两天中至少有一天空气质量指数在区间
表示事件“在本月空气质量指数大于等于91的这些天中随机选取两天,这两天中至少有一天空气质量指数在区间![]() 内”,
内”,
由己知,质量指数在区间![]() 内的有3天,
内的有3天,
记这三天分别为![]() ,
,
质量指数在区间![]() 内的有2天,
内的有2天,
记这两天分别为![]() ,
,
则选取的所有可能结果为: ![]()
基本事件数为10.
事件“至少有一天空气质量指数在区间![]() 内”的可能结果为:
内”的可能结果为: ![]()
基本事件数为 7,
所以![]()


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() 与
与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的圆的切线为
的圆的切线为![]() 是圆上异于
是圆上异于![]() 的一点,
的一点,![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 是
是![]() 的中点,延长
的中点,延长![]() 分别交
分别交![]() 于
于![]() .
.

(1)若点![]() ,求以
,求以![]() 为直径的圆的方程,并判断
为直径的圆的方程,并判断![]() 是否在圆上;
是否在圆上;
(2)当![]() 在圆上运动时,证明:直线
在圆上运动时,证明:直线![]() 恒与圆
恒与圆![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在透明塑料制成的长方体![]() 容器内灌进一些水(未满),现将容器底面一边
容器内灌进一些水(未满),现将容器底面一边![]() 固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:
固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:
①水的部分始终呈棱柱状;
②水面四边形![]() 的面积为定值;
的面积为定值;
③棱![]() 始终与水面
始终与水面![]() 平行;
平行;
④若![]() ,
, ![]() ,则
,则![]() 是定值.
是定值.
则其中正确命题的个数的是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
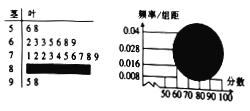
【题目】如图,某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分,据此解答如下问题:
(1)求该班全体男生的人数及分数在![]() 之间的男生人数;
之间的男生人数;
(2)根据频率分布直方图,估计该班全体男生的数学平均成绩(同一组中的数据用该组区间的中点值代表);
(3)从分数在![]() 中抽取两个男生,求抽取的两男生分别来自
中抽取两个男生,求抽取的两男生分别来自![]() 、
、![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经测算,某型号汽车在匀速行驶过程中每小时耗油量![]() (升)与速度
(升)与速度![]() (千米/每小时)
(千米/每小时) ![]() 的关系可近似表示为:
的关系可近似表示为: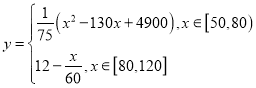 .
.
(Ⅰ)该型号汽车速度为多少时,可使得每小时耗油量最低?
(Ⅱ)已知![]() 两地相距120公里,假定该型号汽车匀速从
两地相距120公里,假定该型号汽车匀速从![]() 地驶向
地驶向![]() 地,则汽车速度为多少时总耗油量最少?
地,则汽车速度为多少时总耗油量最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() ,且函数
,且函数![]() 的最小正周期为
的最小正周期为![]() 。
。
(1)若函数![]() 在
在![]() 处取到最小值
处取到最小值![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)若将函数![]() 图象上所有点的横坐标伸长到原来的
图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),再将向左平移
倍(纵坐标不变),再将向左平移![]() 个单位,得到的函数图象关于
个单位,得到的函数图象关于![]() 轴对称,求函数
轴对称,求函数![]() 的单调递增区间。
的单调递增区间。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率是![]() ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率是![]() ,甲、乙两台机床加工的零件都是一等品的概率是
,甲、乙两台机床加工的零件都是一等品的概率是![]() .
.
(1)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(2)从甲、乙、丙三台机床加工的零件中各取一个检验,求至少有一个一等品的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com