
分析 根据反三角函数的求导公式和复合函数的求导公式求导即可.
解答 解:(1)y=arcsin$\sqrt{x}$,y′=$\frac{1}{\sqrt{1-x}}$•($\sqrt{x}$)′=$\frac{1}{\sqrt{1-x}}$•$\frac{1}{2}\frac{1}{\sqrt{x}}$=$\frac{1}{2\sqrt{x-{x}^{2}}}$=$\frac{\sqrt{x-{x}^{2}}}{2x-2{x}^{2}}$,
(2)y=arccos2x,y′=-$\frac{1}{\sqrt{1-4{x}^{2}}}$•(2x)′=-$\frac{2\sqrt{1-4{x}^{2}}}{1-4{x}^{2}}$,
(3)y=arctan$\frac{1}{x}$,y′=$\frac{1}{1+(\frac{1}{x})^{2}}$•$(\frac{1}{x})′$=$\frac{{x}^{2}}{{x}^{2}+1}$•(-$\frac{1}{{x}^{2}}$)=-$\frac{1}{{x}^{2}+1}$
(4)y=arccot(3x-1),y′=-$\frac{1}{1+(3x-1)^{2}}$•(3x-1)′=-$\frac{3}{1+(3x-1)^{2}}$
点评 本题考查了反三角函数的求导公式和复合函数的求导公式,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 3 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
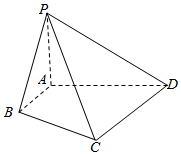 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD中,∠A=90°,AB∥CD,AB=1,AD=CD=2.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD中,∠A=90°,AB∥CD,AB=1,AD=CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (0,4) | C. | ($\frac{1}{4}$,4) | D. | (4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com