
已知抛物线方程为 ,过点
,过点
 作直线与抛物线交于两点
作直线与抛物线交于两点 ,
,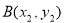 ,过
,过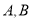 分别作抛物线的切线,两切线的交点为
分别作抛物线的切线,两切线的交点为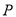 .
.
(1)求 的值;
的值;
(2)求点 的纵坐标;
的纵坐标;
(3)求△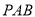 面积的最小值.
面积的最小值.
(1)-8;(2)-2:(3)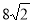 .
.
【解析】
试题分析:
解题思路:(1)联立直线与抛物线方程,整理得到关于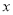 的一元二次方程,利用根与系数的关系求两根之积即可;(2)由导数的几何意义求切线方程,联立方程,解方程组即得P点纵坐标;(3)求弦长和面积,再利用基本不等式求最值.
的一元二次方程,利用根与系数的关系求两根之积即可;(2)由导数的几何意义求切线方程,联立方程,解方程组即得P点纵坐标;(3)求弦长和面积,再利用基本不等式求最值.
规律总结:直线与抛物线的位置关系,是高考数学的重要题型,其一般思路是联立直线与抛物线的方程,整理得到关于或的一元二次方程,采用“设而不求”的方法进行解答,综合型较强.
试题解析:(1)由已知直线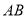 的方程为
的方程为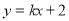 ,代入
,代入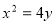 得
得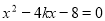 ,
,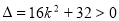 ,∴
,∴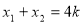 ,
,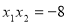 .
.
(2)由导数的几何意义知过点 的切线斜率为
的切线斜率为 ,
,
∴切线方程为 ,化简得
,化简得 ①
①
同理过点 的切线方程为
的切线方程为 ②
②
由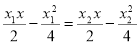 ,得
,得 , ③
, ③
将③代入①得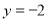 ,∴点
,∴点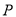 的纵坐标为
的纵坐标为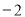 .
.
(3)设直线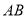 的方程为
的方程为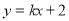 ,
,
由(1)知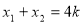 ,
,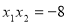 ,
,
∵点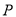 到直线
到直线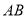 的距离为
的距离为 ,
,
线段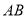 的长度为
的长度为
 .
. 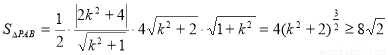 ,
,
当且仅当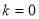 时取等号,∴△
时取等号,∴△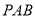 面积的最小值为
面积的最小值为 .
.
考点:直线与抛物线的位置关系.


科目:高中数学 来源:2015数学一轮复习迎战高考:10-6几何概型(解析版) 题型:选择题
[2012·北京高考]设不等式组 ,表示平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )
,表示平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是( )
A. B.
B.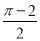 C.
C. D.
D.

查看答案和解析>>
科目:高中数学 来源:2015数学一轮复习迎战高考1-3简单逻辑联结词、全称量词与存在量词(解析版) 题型:选择题
[2014·孝感统考]已知命题p:?x∈R,使sinx=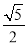 ;命题q:?x∈R,都有x2+x+1>0.给出下列结论:
;命题q:?x∈R,都有x2+x+1>0.给出下列结论:
①命题p∧q是真命题;②命题( p)∨q是真命题;③命题(
p)∨q是真命题;③命题(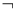 p)∨(
p)∨(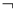 q)是假命题;④命题p∧(
q)是假命题;④命题p∧(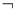 q)是假命题.
q)是假命题.
其中正确的是( )
A.②③ B.②④ C.③④ D.①②③
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( ).
A.y=cos2x,x∈R B.y=log2|x|,x∈R且x≠0)
C.y=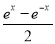 ,x∈R D.y=x3+1,x∈R
,x∈R D.y=x3+1,x∈R
查看答案和解析>>
科目:高中数学 来源:2015届黑龙江省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知函数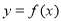 的周期为2,当
的周期为2,当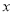 ∈[-1,1]时
∈[-1,1]时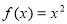 ,那么函数
,那么函数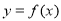 的图象与函数
的图象与函数 的图象的交点共有( ).
的图象的交点共有( ).
A、10个 B、9个 C、8个 D、1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com