
分析 (1)切线l的斜率存在时设为k,则该直线的方程可设为:y=k(x-4)⇒kx-y-4k=0,利用圆的切线的性质:圆心到切线的距离d=r即可得出k.斜率不存在时判断即可.
(2)设这样的直线存在,其方程为y=x+b,代入圆的方程,利用根与系数的关系求得x1+x2,x1•x2的值,进而求得y1•y2的值.根据OA⊥OB得x1x2+y1y2=0,求得b=1,或b=-4,从而得出结论.
解答 解:切线l的斜率存在时设为k,则该直线的方程可设为:y=k(x-4)⇒kx-y-4k=0,
由圆的方程为x2+y2-2x+4y-4=0,配方得(x-1)2+(y+2)2=9,可得圆心C(1,-2),半径r=3.
由圆的切线的性质可得:$\frac{|k+2-4k|}{\sqrt{1+{k}^{2}}}$=3,解得k=-$\frac{5}{12}$.此时的切线方程为:5x+12y-20=0.
当切线的斜率不存在时,切线为:x=4.满足题意,
所以有点切线方程为:x=4或5x+12y-20=0
(2)假设存在以AB为直径的圆M,圆心M的坐标为(a,b)
由于CM⊥m,∴kCM?km=-1∴kCM=$\frac{b+2}{a-1}=-1$,(6分)
即a+b+1=0,得b=-a-1 ①
直线m的方程为y-b=x-a,即x-y+b-a=0 (8分)
CM=$\frac{{|{b-a+3}|}}{{\sqrt{2}}}$(10分)
∵以AB为直径的圆M过原点,∴|MA|=|MB|=|OM|${|{MB}|^2}={|{CB}|^2}-{|{CM}|^2}=9-\frac{{{{(b-a+3)}^2}}}{2}$,
|OM|2=a2+b2
∴$9-\frac{{{{(b-a+3)}^2}}}{2}={a^2}+{b^2}$②(12分)
把①代入②得 2a2-a-3=0,∴a=$\frac{3}{2}$或a=-1 (13分)
当a=$\frac{3}{2}$时,b=-$\frac{5}{2}$此时直线m的方程为x-y-4=0;
当a=-1时,b=0此时直线m的方程为x-y+1=0
故这样的直线l是存在的,方程为x-y-4=0 或x-y+1=0.
点评 本题主要考查求圆的切线方程,直线和圆的位置关系应用,一元二次方程根与系数的关系,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
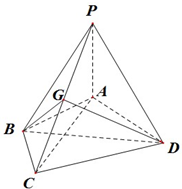 如图,四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=120°,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,G为线段PC上的点.
如图,四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=120°,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,G为线段PC上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com