
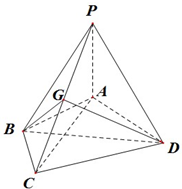
 如图,四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=120°,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,G为线段PC上的点.
如图,四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=120°,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,G为线段PC上的点.分析 (Ⅰ)由PA⊥面ABCD,可得PA⊥BD;设AC与BD的交点为O,则由条件可得BD是AC的中垂线,故O为AC的中点,且BD⊥AC.再利用直线和平面垂直的判定定理证得BD⊥面PAC.
(Ⅱ)先证 PC⊥OG,且PC=$\sqrt{15}$由△COG∽△CAP,可得$\frac{GC}{AC}=\frac{OC}{PC}$,解得GC的值,可得PG
=PC-GC 的值,从而求得$\frac{PG}{GC}$ 的值.
(Ⅲ)由三角形的中位线性质以及条件证明∠DGO为DG与平面PAC所成的角,求出GO和AC的值,可得OC、OD的值,再利用直角三角形中的边角关系求得tan∠DGO的值.
解答 (Ⅰ)证明:∵在四棱锥P-ABCD中,PA⊥面ABCD,∴PA⊥BD.
∵AB=BC=2,AD=CD=$\sqrt{7}$,设AC与BD的交点为O,则BD是AC的中垂线,故O为AC的中点,且BD⊥AC.
而PA∩AC=A,∴BD⊥面PAC.
(Ⅱ)解:若G满足PC⊥面BGD,∵OG?平面BGD,∴PC⊥OG,且 PC=$\sqrt{15}$
由△COG∽△CPA,可得$\frac{GC}{AC}=\frac{OC}{PC}$,解得GC=$\frac{2\sqrt{15}}{5}$,
∴PG=PC-GC=$\sqrt{15}-\frac{2\sqrt{15}}{5}$=$\frac{3\sqrt{15}}{5}$,∴$\frac{PG}{GC}$=$\frac{3}{2}$.
(Ⅲ)解:若G是PC的中点,O为AC的中点,则GO平行且等于$\frac{1}{2}$PA,故由PA⊥面ABCD,可得GO⊥面ABCD,
∴GO⊥OD,故OD⊥平面PAC,故∠DGO为DG与平面PAC所成的角.
由题意可得,GO=$\frac{1}{2}$PA=$\frac{\sqrt{3}}{2}$
△ABC中,由余弦定理可得AC2=AB2+BC2-2AB•BC•cos∠ABC=4+4-2×2×2×cos120°=12,
∴AC=2$\sqrt{3}$,OC=$\sqrt{3}$.
∵直角三角形COD中,OD=2,
∴直角三角形GOD中,tan∠DGO=$\frac{OD}{OG}$=$\frac{4\sqrt{3}}{3}$.
点评 本题主要考查直线和平面垂直的判定定理的应用,求直线和平面所成的角,空间距离的求法,属于中档题.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:选择题
 如图,四棱锥PABCD的底面是边长为8的正方形,四条侧棱长均为2$\sqrt{17}$.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.若EB=2,则四边形GEFH的面积为( )
如图,四棱锥PABCD的底面是边长为8的正方形,四条侧棱长均为2$\sqrt{17}$.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.若EB=2,则四边形GEFH的面积为( )| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{\sqrt{e}}{e}$-8] | B. | [$\frac{\sqrt{e}}{e}$-8,+∞) | C. | [$\sqrt{2}$,e) | D. | (-$\frac{\sqrt{3}}{3}$,$\frac{e}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | (1,+∞) | C. | [0,1) | D. | [0,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com