
| A. | (-∞,$\frac{\sqrt{e}}{e}$-8] | B. | [$\frac{\sqrt{e}}{e}$-8,+∞) | C. | [$\sqrt{2}$,e) | D. | (-$\frac{\sqrt{3}}{3}$,$\frac{e}{2}$) |
分析 先将问题等价为:f'(x)max≤g(x)max,再分别对二次函数和指数函数在相应区间上求最值.
解答 解:根据题意,要使得f'(x1)≤g(x2)成立,
只需满足:f'(x)max≤g(x)max,
而f'(x)=x2+2x+a=(x+1)2+a-1,x∈[$\frac{1}{2}$,2],
所以,f'(x)max=f(2)=a+8,
g(x)=e-x,x∈[$\frac{1}{2}$,2],函数单调递减,
所以,g(x)max=g($\frac{1}{2}$)=${e}^{-\frac{1}{2}}$,
因此,a+8≤${e}^{-\frac{1}{2}}$,解得a≤${e}^{-\frac{1}{2}}$-8=$\frac{\sqrt{e}}{e}$-8,
所以,实数a的取值范围为:(-∞,$\frac{\sqrt{e}}{e}$-8],
故选:A.
点评 本题主要考查了不等式有解和恒成立的综合问题,涉及二次函数和指数函数的单调性和值域,以及导数的运算,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 4 | C. | 8(log23-1) | D. | $-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
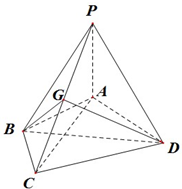 如图,四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=120°,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,G为线段PC上的点.
如图,四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=120°,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,G为线段PC上的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | $[-2,-\frac{1}{2}]$∪$[\frac{1}{2},2]$ | C. | $[-\frac{1}{2},0)$∪$(0,\frac{1}{2}]$ | D. | (-∞,-2]∪[2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com