
分析 首先判断f(x)>0在定义域上恒成立;有 $lo{g}_{2}(x-{2}^{m}+\frac{5}{4})$>0,即x-2m+$\frac{5}{4}$>1恒成立,则x>2m-$\frac{1}{4}$恒成立.
解答 解:由题意知:f'(x)=cosx-$\frac{1}{2}$,当0<x<1时,f'(x)>0,即函数f(x)在(0,1)单调递增,此时f(0)=0;
又不等式f(x)•$lo{g}_{2}(x-{2}^{m}+\frac{5}{4})$>0恒成立.
∴$lo{g}_{2}(x-{2}^{m}+\frac{5}{4})$>0,即x-2m+$\frac{5}{4}$>1恒成立,则x>2m-$\frac{1}{4}$恒成立,
∵0<x<1,
∴2m-$\frac{1}{4}$≤0⇒m≤-2.
故答案为:(-∞,-2]
点评 本题主要考查了函数的单调性与最值,不等式与对数的基础运算,属于中等题.


科目:高中数学 来源: 题型:解答题
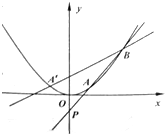 已知抛物线C:x2=2py(p>0)过点(2,1),直线l过点P(0,-1)与抛物线C交于A、B两点,点A关于y轴的对称点为A′,连接A′B
已知抛物线C:x2=2py(p>0)过点(2,1),直线l过点P(0,-1)与抛物线C交于A、B两点,点A关于y轴的对称点为A′,连接A′B查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
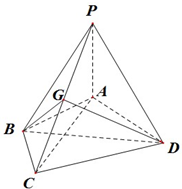 如图,四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=120°,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,G为线段PC上的点.
如图,四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=120°,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,G为线段PC上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9<m<25 | B. | 8<m<25 | C. | 16<m<25 | D. | m>8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com