
分析 (1)由题意f(1)=$\frac{5}{2}$,f(2)=$\frac{17}{4}$,带入计算即可求出p,q的值,可得函数f(x)的解析式.
(2)直接利用定义法证明单调性.
(3)当x∈(0,$\frac{1}{2}}$]时,函数f(x)的最小值,即f(x)min≥2-m成立求实数m的取值范围.
解答 解:(1)由题意:函数f(x)=px+$\frac{q}{x}$(实数p、q为常数),
∵$\left\{\begin{array}{l}f(1)=\frac{5}{2}\\ f(2)=\frac{17}{4}\end{array}\right.$,
∴$\left\{\begin{array}{l}p+q=\frac{5}{2}\\ 2p+\frac{q}{2}=\frac{17}{4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}p=2\\ q=\frac{1}{2}\end{array}\right.$,
故得:函数f(x)的解析式:f(x)=$2x+\frac{1}{2x}$.
(2)由(1)可知f(x)=$2x+\frac{1}{2x}$,
∴在区间(0,$\frac{1}{2}}$]上的单调递减.
证明:设$0<{x}_{1}<{x}_{2}<\frac{1}{2}$;
f(x1)-f(x2)=$2{x}_{1}-2{x}_{2}+\frac{1}{2{x}_{1}}-\frac{1}{2{x}_{2}}$=2(x1-x2)$+\frac{{x}_{2}-{x}_{1}}{2{x}_{1}{x}_{2}}$=$({x}_{2}-{x}_{1})(-2+\frac{1}{2{x}_{1}{x}_{2}})$=(x2-x1)$\frac{1-4{x}_{1}{x}_{2}}{2{x}_{1}{x}_{2}}$
∵$0<{x}_{1}<{x}_{2}<\frac{1}{2}$;
∴0<x2x1$<\frac{1}{4}$,1-4x1x2>0
则:f(x1)-f(x2)>0
所以:f(x)=$2x+\frac{1}{2x}$在区间(0,$\frac{1}{2}}$]上的单调递减.
(3)由(2)可知当x∈(0,$\frac{1}{2}}$]时,函数f(x)是单调减函数
∴当x=$\frac{1}{2}$时,函数f(x)取得最小值,即f(x)min=f$(\frac{1}{2})$=2
要使x∈(0,$\frac{1}{2}}$]时,函数f(x)≥2-m恒成立,
只需f(x)min≥2-m成立,
即:2≥2-m,
解得:m≥0
故得实数m的取值范围[0,+∞).
点评 本题考查了函数的解析式的求法和恒成立转化为不等式求解的问题.属于中档题.


科目:高中数学 来源: 题型:填空题
 如图是一个几何体的侧视图和俯视图,已知俯视图中的两个而矩形是全等的,且该几何体的正视图是一个正方形,则该几何体的表面积为4$+4\sqrt{3}$.
如图是一个几何体的侧视图和俯视图,已知俯视图中的两个而矩形是全等的,且该几何体的正视图是一个正方形,则该几何体的表面积为4$+4\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
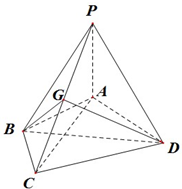 如图,四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=120°,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,G为线段PC上的点.
如图,四棱锥P-ABCD中,PA⊥面ABCD,∠ABC=120°,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,G为线段PC上的点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{32}$ | B. | $\frac{3}{16}$ | C. | 48 | D. | 94 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com