
分析 由于X~B(n,p),且E(X)=6,D(X)=$\frac{9}{2}$,可得np=6,np(1-p)=$\frac{9}{2}$,解得n=24.则在$(\sqrt{x}+\frac{1}{\root{3}{x}})^{24}$的展开式中,利用其通项公式即可得出结论.
解答 解:∵X~B(n,p),且E(X)=6,D(X)=$\frac{9}{2}$,
∴np=6,np(1-p)=$\frac{9}{2}$,解得n=24.
则在$(\sqrt{x}+\frac{1}{\root{3}{x}})^{24}$的展开式中,通项公式Tr+1=${∁}_{24}^{r}(\sqrt{x})^{24-r}$$(\frac{1}{\root{3}{x}})^{r}$=${∁}_{24}^{r}{x}^{12-\frac{5r}{6}}$,r=0,1,2,…,24.
当且仅当r=0,6,12,18,24时,Tr+1为有理项.
因此有理项共有5项,
故答案为:5.
点评 本题考查了二项分布的性质、二项式定理的通项公式及其应用,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 平行于同一直线的两个平面平行 | B. | 垂直于同一直线的两个平面平行 | ||
| C. | 平行于同一平面的两条直线平行 | D. | 垂直于同一直线的两条直线平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 定义:若曲线τ由椭圆T1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和椭圆T2:$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(b>c>0)组成,当a、b、c成等比数列时,称曲线τ为“猫眼曲线”.若“猫眼曲线”τ过点P(0,-$\sqrt{2}$),且a、b、c的公比为$\frac{\sqrt{2}}{2}$.
定义:若曲线τ由椭圆T1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和椭圆T2:$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(b>c>0)组成,当a、b、c成等比数列时,称曲线τ为“猫眼曲线”.若“猫眼曲线”τ过点P(0,-$\sqrt{2}$),且a、b、c的公比为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
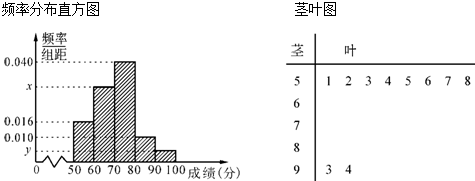
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
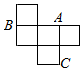 一个无盖的正方体盒子展开后的平面图如图所示,A、B、C是展开图上的三点,则在正方体盒子中,∠ABC的度数是( )
一个无盖的正方体盒子展开后的平面图如图所示,A、B、C是展开图上的三点,则在正方体盒子中,∠ABC的度数是( )| A. | 45° | B. | 30° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com