
 定义:若曲线τ由椭圆T1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和椭圆T2:$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(b>c>0)组成,当a、b、c成等比数列时,称曲线τ为“猫眼曲线”.若“猫眼曲线”τ过点P(0,-$\sqrt{2}$),且a、b、c的公比为$\frac{\sqrt{2}}{2}$.
定义:若曲线τ由椭圆T1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和椭圆T2:$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(b>c>0)组成,当a、b、c成等比数列时,称曲线τ为“猫眼曲线”.若“猫眼曲线”τ过点P(0,-$\sqrt{2}$),且a、b、c的公比为$\frac{\sqrt{2}}{2}$.分析 (1)由题意可知:b=$\sqrt{2}$,$\frac{b}{a}$=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,代入分别求得a和c的值,即可求得“猫眼曲线”τ的方程;
(2)根据中点坐标公式,将E,F坐标代入椭圆方程,利用”点差法“求得k•kOM=-$\frac{1}{2}$,同理求得k•kON=-2,即可求得$\frac{{k}_{OM}}{{k}_{ON}}$的值;
(3)设直线方程y=x+m,分别代入T1和T2,求得关于x的一元二次方程,根据根与系数的关系,利用弦长公式分别求得丨AB丨和丨CD丨,根据$\frac{|AB|}{|CD|}$=2,即可求得m的值,求得直线方程.
解答 解:(1)由题意知,b=$\sqrt{2}$,$\frac{b}{a}$=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
∴a=2,c=1,
∴T1:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1,T2:$\frac{{y}^{2}}{2}$+x2=1.
(2)设斜率为k(k≠0)的直线交椭圆T1于点E(x1,y1),F(x2,y2)线段EF中点为M(x0,y0),
则x0=$\frac{{x}_{1}+{x}_{2}}{2}$,y0=$\frac{{y}_{1}+{y}_{2}}{2}$,
由$\left\{\begin{array}{l}{\frac{{x}_{1}^{2}}{4}+\frac{{y}_{1}^{2}}{2}=1}\\{\frac{{x}_{2}^{2}}{4}+\frac{{y}_{2}^{2}}{2}=1}\end{array}\right.$,得$\frac{({x}_{1}-{x}_{2})({x}_{1}+{x}_{2})}{4}$+$\frac{({y}_{1}-{y}_{2})({y}_{1}+{y}_{2})}{2}$=0,
因为k存在且k≠0,
∴x1≠x2,x0≠0,
∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$-$\frac{{y}_{0}}{{x}_{0}}$=-$\frac{1}{2}$,即k•kOM=-$\frac{1}{2}$,
同理k•kON=-2,
∴$\frac{{k}_{OM}}{{k}_{ON}}$=$\frac{1}{4}$;
(3)设直线l的方程为:y=x+m,A(xA,yA),B(xB,yB),C(xA,yA),D(xB,yB),
由$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,得3x2+4mx+2m2-4=0,
由韦达定理可知:xA+xB=-$\frac{4m}{3}$,xA•xB=$\frac{2{m}^{2}-4}{3}$,
由$\left\{\begin{array}{l}{y=x+m}\\{\frac{{y}^{2}}{2}+{x}^{2}=1}\end{array}\right.$,得3x2+2mx+m2-2=0,
由韦达定理可知:xC+xD=-$\frac{2m}{3}$,xC•xD=$\frac{{m}^{2}-2}{3}$,
∴$\frac{|AB|}{|CD|}$=$\frac{\sqrt{1+{k}^{2}}丨{x}_{A}-{x}_{B}丨}{\sqrt{1+{k}^{2}}丨{x}_{C}-{x}_{D}丨}$=$\frac{\sqrt{({x}_{A}-{x}_{B})^{2}-4{x}_{A}{x}_{B}}}{\sqrt{({x}_{C}-{x}_{D})^{2}-4{x}_{C}{x}_{D}}}$=$\frac{\sqrt{48-8{m}^{2}}}{\sqrt{24-8{m}^{2}}}$=2,
解得:m=±$\sqrt{2}$,
所以直线l的方程为y=x±$\sqrt{2}$.
点评 本题考查直线与椭圆位置关系的综合应用,考查一元二次方程根与系数的关系、弦长公式,考查直线方程的求得,考查综合运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
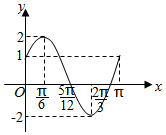 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
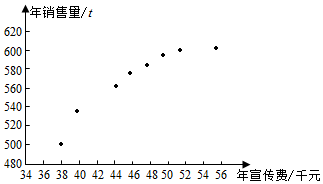 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum_{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum_{i=1}^{8}$(wi-$\overline{w}$)2 | $\sum_{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum_{i=1}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com