
分析 (1)先解不等式,再利用不等式f(x)≤2的解集为单元素集,求实数m的值;
(2)存在x0∈R,使得f(x0)+f(-x0)≤a成立,则|x0-1|+2+|-x0-1|+2≤a,即|x0-1|+|-x0-1|≤a-4,求出左边的最小值,即可求实数a的取值范围.
解答 解:(1)由题意|x-m|≤2-2m,
∴3m-2≤x≤2-m,
∵不等式f(x)≤2的解集为单元素集,
∴3m-2=2-m,
∴m=1;
(2)f(x)=|x-1|+2,
存在x0∈R,使得f(x0)+f(-x0)≤a成立,则|x0-1|+2+|-x0-1|+2≤a,
∴|x0-1|+|-x0-1|≤a-4,
∵|x0-1|+|-x0-1|≥|x0-1-x0-1|=2,
∴a-4≥2,
∴a≥6.
点评 本题考查绝对值不等式,考查学生分析解决问题的能力,正确转化是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 定义:若曲线τ由椭圆T1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和椭圆T2:$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(b>c>0)组成,当a、b、c成等比数列时,称曲线τ为“猫眼曲线”.若“猫眼曲线”τ过点P(0,-$\sqrt{2}$),且a、b、c的公比为$\frac{\sqrt{2}}{2}$.
定义:若曲线τ由椭圆T1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和椭圆T2:$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(b>c>0)组成,当a、b、c成等比数列时,称曲线τ为“猫眼曲线”.若“猫眼曲线”τ过点P(0,-$\sqrt{2}$),且a、b、c的公比为$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
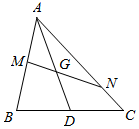 如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB、AC于M、N两点.若$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则$\frac{1}{x}$+$\frac{1}{y}$=4.
如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN分别交AB、AC于M、N两点.若$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则$\frac{1}{x}$+$\frac{1}{y}$=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com