
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 ①根据分式不等式的解法进行求解判断,
②根据否命题的定义进行判断,
③根据全称命题的否定是特称命题进行判断,
④根据一元二次方程与判别式△的关系结合充分条件和必要条件的定义进行判断.
解答 解:①命题“关于x的不等式$\frac{1-x}{1+x}$≥0的解集为{x|-1<x≤1}”,故①错误;
②命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;故②正确,
③命题“?x∈R,x2+1≥1”的否定是““?x∈R,x2+1<1”;故③错误,
④若方程x2+x+m=0有实数解,则判别式△=1-4m≥0,则m≤$\frac{1}{4}$,
即“m<$\frac{1}{4}$”是“方程x2+x+m=0有实数解”的充分不必要条件,故④错误,
故①③④错误;
故选:B
点评 本题主要考查命题的真假判断,涉及知识点较多,综合性较强,难度不大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
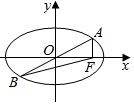 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),过原点的直线与椭圆交于A、B两点,点F为椭圆的右焦点,且满足AF⊥BF,设∠ABF=α,且α∈[$\frac{π}{12}$,$\frac{π}{6}$],则椭圆离心率e的取值范围为( )
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),过原点的直线与椭圆交于A、B两点,点F为椭圆的右焦点,且满足AF⊥BF,设∠ABF=α,且α∈[$\frac{π}{12}$,$\frac{π}{6}$],则椭圆离心率e的取值范围为( )| A. | [$\sqrt{3}$-1,$\frac{2}{3}$] | B. | [$\sqrt{3}$-1,$\frac{\sqrt{6}}{3}$] | C. | [2-$\sqrt{3}$,$\frac{2}{3}$] | D. | [2-$\sqrt{3}$,$\frac{\sqrt{6}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{15}$ | B. | $\frac{2}{15}$ | C. | $-\frac{2}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
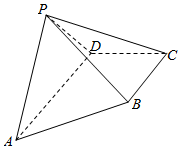 如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2CD=2,侧面APD为等腰直角三角形,PA⊥PD,平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,AD∥BC,AD⊥DC,AD=2BC=2CD=2,侧面APD为等腰直角三角形,PA⊥PD,平面PAD⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com