
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{2}$-p | p | $\frac{1}{2}$ |
分析 根据所给的分布列的性质,即每一个概率都在[0,1)之间,写出关于概率P的不等式组,解出P的范围,写出期望和方差的表示式,根据P的范围,求出最值.
解答 解:由随机变量ξ的分布列的性质,得:
$\left\{\begin{array}{l}{0≤\frac{1}{2}-p≤1}\\{0≤p≤1}\end{array}\right.$,解得0≤p$≤\frac{1}{2}$,
∴Eξ=p+1,
Dξ=(0-p-1)2×$\frac{1}{2}$+(1-p-1)2×p+(2-p-1)2×$\frac{1}{2}$=-p2-p+1=-(p+$\frac{1}{2}$)2+$\frac{5}{4}$.
∴当P=0时,Dξ取最大值(Dξ)max=-$\frac{1}{4}+\frac{5}{4}$=1.
故答案为:1.
点评 本题考查离散型随机变量的数学期望的最大值和方差的最小值的求法,是中档题,解题时要注意分布列的性质和配方法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
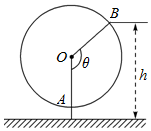 (1,3班做)一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面间的距离为h.
(1,3班做)一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面间的距离为h.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com