
设等差数列 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则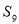 等于
等于
A. B.
B. C.
C. D.
D.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年贵州省高三模拟考试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数
 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)在锐角三角形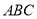 中,a、b、c分别是角A、B、C的对边,若
中,a、b、c分别是角A、B、C的对边,若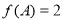 ,
, ,
, 的面积为
的面积为 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市高二上学期第一次月考数学试卷(解析版) 题型:解答题
已知正项数列 ,
, ,且
,且
(1)求证: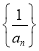 是等差数列,并求
是等差数列,并求 的通项公式;
的通项公式;
(2)数列 满足
满足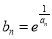 ,若
,若 ,仍是
,仍是 中的项,求
中的项,求 在区间
在区间 中的所有可能值之和
中的所有可能值之和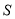 ;
;
(3)若将上述递推关系 改为:
改为: ,且数列
,且数列 中任意项
中任意项 ,试求满足要求的实数
,试求满足要求的实数 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市高二上学期第一次月考数学试卷(解析版) 题型:选择题
设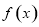 是定义在
是定义在 上恒不为零的函数,且对任意的实数
上恒不为零的函数,且对任意的实数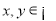 ,都有
,都有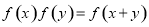 ,若
,若 ,
, ,则数列
,则数列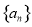 的前
的前 项和
项和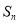 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷(解析版) 题型:填空题
底面直径为10的圆柱被与底面成60°的平面所截,截口是一个椭圆,该椭圆的长轴长 ,短轴长 ,离心率为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-3 2.2超几何分布练习卷(解析版) 题型:解答题
(2009•朝阳区二模)在袋子中装有10个大小相同的小球,其中黑球有3个,白球有n(2≤n≤5,且n≠3)个,其余的球为红球.
(Ⅰ)若n=5,从袋中任取1个球,记下颜色后放回,连续取三次,求三次取出的球中恰有2个红球的概率;
(Ⅱ)从袋里任意取出2个球,如果这两个球的颜色相同的概率是 ,求红球的个数;
,求红球的个数;
(Ⅲ)在(Ⅱ)的条件下,从袋里任意取出2个球.若取出1个白球记1分,取出1个黑球记2分,取出1个红球记3分.用ξ表示取出的2个球所得分数的和,写出ξ的分布列,并求ξ的数学期望Eξ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com