
【题目】已知非零数列![]() 的递推公式为
的递推公式为![]() ,
,![]() .
.
(1)求证数列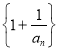 是等比数列;
是等比数列;
(2)若关于![]() 的不等式
的不等式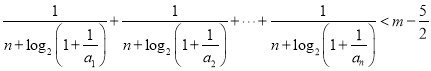 有解,求整数
有解,求整数![]() 的最小值;
的最小值;
(3)在数列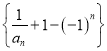 中,是否一定存在首项、第
中,是否一定存在首项、第![]() 项、第
项、第![]() 项
项![]() ,使得这三项依次成等差数列?若存在,请指出
,使得这三项依次成等差数列?若存在,请指出![]() 所满足的条件;若不存在,请说明理由.
所满足的条件;若不存在,请说明理由.
【答案】(1)证明见解析(2)整数![]() 的最小值为4.(3)存在,当且仅当
的最小值为4.(3)存在,当且仅当![]() ,且
,且![]() 为不小于4的偶数时,
为不小于4的偶数时,![]() 成等差数列
成等差数列
【解析】
(1)根据要证明是等比数列的数列,对已知的等式进行恒等变形,即可证明本结论;
(2)利用差比判断数列的单调性,利用单调性求出整数![]() 的最小值;
的最小值;
(3)根据(1)求出数列![]() 的通项公式,结合已知,可以证明出存在首项、第
的通项公式,结合已知,可以证明出存在首项、第![]() 项、第
项、第![]() 项
项![]() ,使得这三项依次成等差数列.
,使得这三项依次成等差数列.
(1)由![]() ,得
,得![]() ,
,
即![]() ,所以
,所以![]() 是首项为2,公比为2的等比数列.
是首项为2,公比为2的等比数列.
(2)由(1)可得:![]() ,所以已知的不等式等价于
,所以已知的不等式等价于![]()
令![]() ,
,
则![]() ,
,
所以![]() 单调递增,则
单调递增,则
![]() ,
,
于是![]() ,即
,即![]() ,故整数
,故整数![]() 的最小值为4.
的最小值为4.
(3)由上面得![]() ,则
,则![]()
要使![]() 成等差数列,只需
成等差数列,只需![]() ,
,
即![]()
因为![]() ,则上式左端
,则上式左端![]() ;又因为上式右端
;又因为上式右端![]()
于是当且仅当![]() ,且
,且![]() 为不小于4的偶数时,
为不小于4的偶数时,![]() 成等差数列.
成等差数列.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过![]() 、
、![]() 、
、![]() 三点.
三点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 、
、![]() 两点,证明直线
两点,证明直线![]() 与直线
与直线![]() 的交点在直线
的交点在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件) | 产品B(件) | ||
研制成本与塔载 | 20 | 30 | 计划最大资 |
产品重量(千克/件) | 10 | 5 | 最大搭载 |
预计收益(万元/件) | 80 | 60 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家,大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(以弦为边长得到的正方形由4个全等的直角三角形再加上中间的一个小正方形组成的),类比“赵爽弦图”,可类似地构造如图所示的图形,它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形,设![]() ,则( )
,则( )
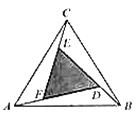
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过定点![]() 且与直线
且与直线![]() 垂直的直线与
垂直的直线与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,点
,点 满足
满足![]() .
.
(1)若以原点为圆心的圆![]() 与
与![]() 有唯一公共点,求圆
有唯一公共点,求圆![]() 的轨迹方程;
的轨迹方程;
(2)求能覆盖![]() 的最小圆的面积;
的最小圆的面积;
(3)在(1)的条件下,点![]() 在直线
在直线![]() 上,圆
上,圆![]() 上总存在两个不同的点
上总存在两个不同的点![]() 使得
使得![]()
![]() 为坐标原点),求
为坐标原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com