
甲,乙两人进行射击比赛,每人射击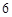 次,他们命中的环数如下表:
次,他们命中的环数如下表:
| 甲 | 5 | 8 | 7 | 9 | 10 | 6 |
| 乙 | 6 | 7 | 4 | 10 | 9 | 9 |
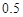 的概率.
的概率. 科目:高中数学 来源: 题型:解答题
将背面相同正面分别标有1、2、3、4的四张卡片洗匀后背面朝上放在桌面上,(1)从中随机的抽取一张卡片,求该卡片正面上的数字是偶数的概率(2)先从中随机的抽取一张卡片(不放回),将该卡片正面上的数字作为十位数字,再随机的抽取一张卡片,将该卡片正面上的数字作为个位数字,则组成的两位数恰好是4的倍数的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有4个人去参加春节联欢活动,该活动有甲、乙两个项目可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个项目联欢,掷出点数为1或2的人去参加甲项目联欢,掷出点数大于2的人去参加乙项目联欢.
(Ⅰ)求这4个人中恰好有2人去参加甲项目联欢的概率;
(Ⅱ)求这4个人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数的概率;
(Ⅲ)用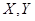 分别表示这4个人中去参加甲、乙项目联欢的人数,记
分别表示这4个人中去参加甲、乙项目联欢的人数,记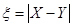 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望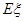 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班数学兴趣小组有男生3名,记为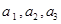 ,女生2名,记为
,女生2名,记为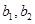 ,现从中任选2名学生去参加校数学竞赛
,现从中任选2名学生去参加校数学竞赛
⑴写出所有的基本事件
⑵求参赛学生中恰好有一名男生的概率
⑶求参赛学生中至少有一名男生的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(Ⅱ)花店记录了100 天玫瑰花的日需求量(单位:枝),整理得下表:
| 日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下表:
| 日销售量(吨) | 1 | 1.5 | 2 |
| 天数 | 10 | 25 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
目前,在我国部分省市出现了人感染H7N9禽流感病毒,为有效防控,2013年4月下旬,北京疫苗研制工作进入动物免疫原性试验阶段。假定现已研制出批号分别为1,2,3,4,5的五批疫苗,准备在A、B、C三种动物身上做试验,给每种动物做实验所选用的疫苗是从这五个批号中任选其中一个批号的疫苗.
(Ⅰ)求给三种动物注射疫苗的批号互不相同的概率;
(Ⅱ)记给A、B、C三种动物注射疫苗的批号最大数为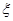 ,求
,求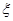 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在1次游戏中,
(i)摸出3个白球的概率;
(ii)获奖的概率;
(Ⅱ)求在2次游戏中获奖次数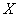 的分布列及数学期望
的分布列及数学期望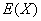
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com