
某班数学兴趣小组有男生3名,记为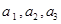 ,女生2名,记为
,女生2名,记为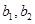 ,现从中任选2名学生去参加校数学竞赛
,现从中任选2名学生去参加校数学竞赛
⑴写出所有的基本事件
⑵求参赛学生中恰好有一名男生的概率
⑶求参赛学生中至少有一名男生的概率
(1)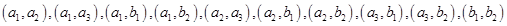
(2)P(A)= 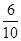 =
=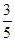 (3)P(B)=1-
(3)P(B)=1-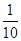 =
=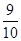
解析试题分析:(1)从中任选2名共有10种情况,即为 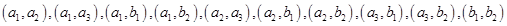 .
.
(2)记“恰有一名男生参赛”为事件A,事件A包含基本事件共有6个,即为(a1,b),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2).所以P(A)=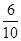 =
=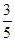 .
.
(3)由题意知本题是一个等可能事件的概率,试验发生所包含的事件数是10,记“至少有一名男生参赛”为事件B,事件B包含基本事件共有9个,即为(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a2,a3),(a2,b1),(a2,b2),(a3,b1),(a3,b2).所以P(B)=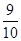 .
.
考点:本题考查了古典概型的运用
点评:本题看出等可能事件的概率和列举法表示出事件所包含的基本事件,本题是一个基础题,解题的关键是列举时要注意做到不重不漏.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
甲、乙两个盒子中各有3个球,其中甲盒中有2个黑球1个白球,乙盒中有1个黑球2个白球,所有球之间只有颜色区别.
(Ⅰ)若从甲、乙两个盒子中各取一个球,求取出的2个球颜色相同的概率;
(Ⅱ)将这两个盒子中的球混合在一起,从中任取2个, 求取出的2个球中至少有一个黑球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某普通高中共有教师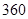 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
| | 第一批次 | 第二批次 | 第三批次 |
| 女教师 | 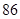 | 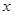 | 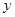 |
| 男教师 | 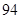 |  | 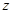 |
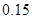 、
、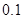 .
.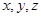 的值;
的值;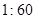 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在进行一项掷骰子放球的游戏中规定:若掷出1点或2点,则在甲盒中放一球;否则,在乙盒中放一球。现在前后一共掷了4次骰子,设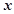 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。
(Ⅰ)求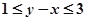 的概率;
的概率;
(Ⅱ)若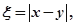 求随机变量
求随机变量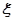 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一个口袋中装有12个大小相同的黑球、白球和红球。已知从袋中任意摸出2个球,至少得到一个黑球的概率是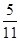 。
。
求:(1)袋中黑球的个数;
(2)从袋中任意摸出3个球,至少得到2个黑球的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一个盒子中,放有大小相同的红、白、黄三个小球,现从中任意摸出一球,若是红球记1分,白球记2分,黄球记3分.现从这个盒子中有放回地先后摸出两球,所得分数分别记为 、
、 ,设
,设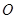 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为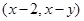 ,记
,记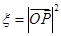 .
.
(1)求随机变量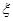 =5的概率;
=5的概率;
(2)求随机变量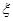 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲,乙两人进行射击比赛,每人射击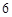 次,他们命中的环数如下表:
次,他们命中的环数如下表:
| 甲 | 5 | 8 | 7 | 9 | 10 | 6 |
| 乙 | 6 | 7 | 4 | 10 | 9 | 9 |
 的概率.
的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为 ,乙队每人答对的概率都是
,乙队每人答对的概率都是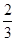 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用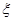 表示甲队总得分.
表示甲队总得分.
(I)求随机变量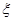 的分布列及其数学期望E(
的分布列及其数学期望E(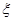 );
);
(Ⅱ)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
)袋中装有大小相同的黑球、白球和红球共10个。已知从袋中任意摸出1个球,得到黑球的概率是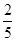 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是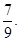
(1)求袋中各色球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的分布列及数学期望Eξ和方差Dξ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com