
在进行一项掷骰子放球的游戏中规定:若掷出1点或2点,则在甲盒中放一球;否则,在乙盒中放一球。现在前后一共掷了4次骰子,设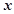 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。
(Ⅰ)求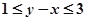 的概率;
的概率;
(Ⅱ)若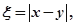 求随机变量
求随机变量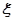 的分布列和数学期望。
的分布列和数学期望。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
甲乙丙三人商量周末去玩,甲提议去市中心逛街,乙提议去城郊觅秋,丙表示随意。最终,商定以抛硬币的方式决定结果。规则是:由丙抛掷硬币若干次,若正面朝上则甲得一分乙得零分,反面朝上则乙得一分甲得零分,先得4分者获胜,三人均执行胜者的提议.记所需抛币次数为 .
.
⑴求 =6的概率;
=6的概率;
⑵求 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的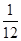 ,
,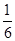 ,
,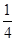 ,
,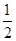 .游戏规则如下:
.游戏规则如下: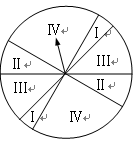
① 当指针指到Ⅰ,Ⅱ, Ⅲ,Ⅳ部分时,分别获得积分100分,40分,10分,0分;
② (ⅰ)若参加该游戏转一次转盘获得的积分不是40分,则按①获得相应的积分,游戏结束;
(ⅱ)若参加该游戏转一次获得的积分是40分,则用抛一枚质地均匀的硬币的方法来决定是否继续游戏.正面向上时,游戏结束;反面向上时,再转一次转盘,若再转一次的积分不高于40分,则最终积分为0分,否则最终积分为100分,游戏结束.
设某人参加该游戏一次所获积分为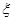 .
.
(1)求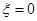 的概率;
的概率;
(2)求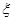 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有 位学生,每次活动均需该系
位学生,每次活动均需该系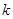 位学生参加(
位学生参加( 和
和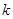 都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系
都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系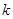 位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为
位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为
(Ⅰ)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(Ⅱ)求使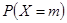 取得最大值的整数
取得最大值的整数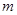 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
现有4个人去参加春节联欢活动,该活动有甲、乙两个项目可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个项目联欢,掷出点数为1或2的人去参加甲项目联欢,掷出点数大于2的人去参加乙项目联欢.
(Ⅰ)求这4个人中恰好有2人去参加甲项目联欢的概率;
(Ⅱ)求这4个人中去参加甲项目联欢的人数大于去参加乙项目联欢的人数的概率;
(Ⅲ)用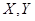 分别表示这4个人中去参加甲、乙项目联欢的人数,记
分别表示这4个人中去参加甲、乙项目联欢的人数,记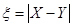 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望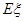 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为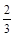
求:(1)乙至少击中目标2次的概率;
(2)乙恰好比甲多击中目标2次的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某班数学兴趣小组有男生3名,记为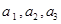 ,女生2名,记为
,女生2名,记为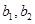 ,现从中任选2名学生去参加校数学竞赛
,现从中任选2名学生去参加校数学竞赛
⑴写出所有的基本事件
⑵求参赛学生中恰好有一名男生的概率
⑶求参赛学生中至少有一名男生的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校在2013年考试成绩中100名学生的笔试成绩的频率分布直方图如图所示,
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙不同时进入第二轮面试的概率;
② 若第三组被抽中的学生实力相当,在第二轮面试中获得优秀的概率均为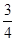 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有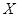 名获得优秀,求
名获得优秀,求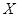 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com