
)袋中装有大小相同的黑球、白球和红球共10个。已知从袋中任意摸出1个球,得到黑球的概率是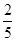 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是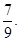
(1)求袋中各色球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的分布列及数学期望Eξ和方差Dξ;
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
某班数学兴趣小组有男生3名,记为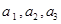 ,女生2名,记为
,女生2名,记为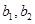 ,现从中任选2名学生去参加校数学竞赛
,现从中任选2名学生去参加校数学竞赛
⑴写出所有的基本事件
⑵求参赛学生中恰好有一名男生的概率
⑶求参赛学生中至少有一名男生的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
目前,在我国部分省市出现了人感染H7N9禽流感病毒,为有效防控,2013年4月下旬,北京疫苗研制工作进入动物免疫原性试验阶段。假定现已研制出批号分别为1,2,3,4,5的五批疫苗,准备在A、B、C三种动物身上做试验,给每种动物做实验所选用的疫苗是从这五个批号中任选其中一个批号的疫苗.
(Ⅰ)求给三种动物注射疫苗的批号互不相同的概率;
(Ⅱ)记给A、B、C三种动物注射疫苗的批号最大数为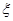 ,求
,求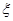 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校在2013年考试成绩中100名学生的笔试成绩的频率分布直方图如图所示,
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙不同时进入第二轮面试的概率;
② 若第三组被抽中的学生实力相当,在第二轮面试中获得优秀的概率均为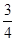 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有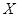 名获得优秀,求
名获得优秀,求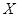 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(Ⅰ)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(Ⅱ)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
哈尔滨市五一期间决定在省妇女儿中心举行中学生“蓝天绿树、爱护环境”围棋比赛,规定如下:
两名选手比赛时每局胜者得1分,负者得0分,比赛进行到有一人比对方多3分或打满7局时停止.
设某学校选手甲和选手乙比赛时,甲在每局中获胜的概率为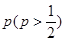 ,且各局胜负相互独立.已知
,且各局胜负相互独立.已知
第三局比赛结束时比赛停止的概率为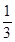 .
.
(1)求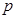 的值;
的值;
(2)求甲赢得比赛的概率;
(3)设 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在1次游戏中,
(i)摸出3个白球的概率;
(ii)获奖的概率;
(Ⅱ)求在2次游戏中获奖次数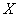 的分布列及数学期望
的分布列及数学期望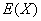
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知关于x的一元二次方程x2-2(a-2)x-b2+16=0.
(1)若a,b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2)若a∈[2,6],b∈[0,4],求方程没有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲乙两人各有一个箱子,甲的箱子里面放有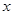 个红球,
个红球,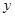 个白球(
个白球( ,且
,且 );乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.
);乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色球的个数,才能使自己获胜的概率最大?并求甲获胜的概率的最大值.
(2) 当甲获胜的概率取得最大值时,求取出的3个球中红球个数 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com