
已知关于x的一元二次方程x2-2(a-2)x-b2+16=0.
(1)若a,b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2)若a∈[2,6],b∈[0,4],求方程没有实根的概率.
(1)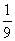 (2)
(2)
解析试题分析:解:(1)基本事件(a,b)共有36个,方程有正根等价于a-2>0,16-b2>0,Δ≥0,
即a>2,-4<b<4,(a-2)2+b2≥16.
设“方程有两个正根”为事件A,则事件A包含的基本事件为(6,1),(6,2),(6,3),(5,3),共4个,
故所求的概率为P(A)= =
=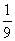 .
.
(2)试验的全部结果构成区域Ω={(a,b)|2≤a≤6,0≤b≤4},
其面积为S(Ω)=16,
设“方程无实根”为事件B,则构成事件B的区域为
B={(a,b)|2≤a≤6,0≤b≤4,(a-2)2+b2<16},
其面积为S(B)= ×π×42=4π,
×π×42=4π,
故所求的概率为P(B)=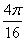 =
=
考点:古典概型的概率
点评:主要是考查了随机事件的概率的运用,属于基础题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为 ,乙队每人答对的概率都是
,乙队每人答对的概率都是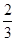 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用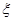 表示甲队总得分.
表示甲队总得分.
(I)求随机变量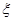 的分布列及其数学期望E(
的分布列及其数学期望E(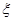 );
);
(Ⅱ)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
)袋中装有大小相同的黑球、白球和红球共10个。已知从袋中任意摸出1个球,得到黑球的概率是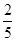 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是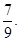
(1)求袋中各色球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为ξ,求随机变量ξ的分布列及数学期望Eξ和方差Dξ;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙、丙三人独立参加某企业的招聘考试,根据三人的专业知识、应试表现、工作经验等综合因素,三人被招聘的概率依次为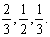 用
用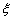 表示被招聘的人数。
表示被招聘的人数。
(1)求三人中至少有一人被招聘的概率;
(2)求随机变量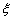 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为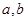 .
.
(1)求直线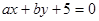 与圆
与圆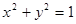 相切的概率;
相切的概率;
(2)将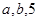 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
哈尔滨市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的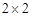 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为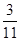 。
。
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
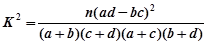 。
。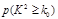 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(1)从1,2,3,4,5五个数中依次取2个数,求这两个数的差的绝对值等于1的概率;
(2)△ABC中,∠B=60°,∠C=45°,高AD=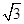 ,在BC边上任取一点M,求
,在BC边上任取一点M,求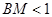 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了保养汽车,维护汽车性能,汽车保养一般都在购车的4S店进行,某地大众汽车4S店售后服务部设有一个服务窗口专门接待保养预约。假设车主预约保养登记所需的时间互相独立,且都是整数分钟,对以往车主预约登记所需的时间统计结果如下:
| 登记所需时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校设计了一个实验考查方案:考生从 道备选题中一次性随机抽取
道备选题中一次性随机抽取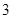 道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中
道题,按照题目要求独立完成全部实验操作.规定:至少正确完成其中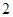 道题的便可通过.已知
道题的便可通过.已知 道备选题中考生甲有
道备选题中考生甲有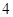 道题能正确完成,
道题能正确完成,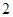 道题不能完成;考生乙每题正确完成的概率都是
道题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)求甲、乙两考生正确完成题数的概率分布列,并计算其数学期望;
(2)请分析比较甲、乙两考生的实验操作能力.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com