
(1)从1,2,3,4,5五个数中依次取2个数,求这两个数的差的绝对值等于1的概率;
(2)△ABC中,∠B=60°,∠C=45°,高AD=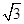 ,在BC边上任取一点M,求
,在BC边上任取一点M,求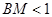 的概率.
的概率.
科目:高中数学 来源: 题型:解答题
目前,在我国部分省市出现了人感染H7N9禽流感病毒,为有效防控,2013年4月下旬,北京疫苗研制工作进入动物免疫原性试验阶段。假定现已研制出批号分别为1,2,3,4,5的五批疫苗,准备在A、B、C三种动物身上做试验,给每种动物做实验所选用的疫苗是从这五个批号中任选其中一个批号的疫苗.
(Ⅰ)求给三种动物注射疫苗的批号互不相同的概率;
(Ⅱ)记给A、B、C三种动物注射疫苗的批号最大数为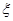 ,求
,求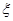 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校游园活动有这样一个游戏项目:甲箱子里装有3个白球、2个黑球,乙箱子里装有1个白球、2个黑球,这些球除颜色外完全相同,每次游戏从这两个箱子里各随机摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(Ⅰ)求在1次游戏中,
(i)摸出3个白球的概率;
(ii)获奖的概率;
(Ⅱ)求在2次游戏中获奖次数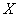 的分布列及数学期望
的分布列及数学期望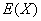
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知关于x的一元二次方程x2-2(a-2)x-b2+16=0.
(1)若a,b是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(2)若a∈[2,6],b∈[0,4],求方程没有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2012年10月1日,为庆祝中华人们共和国成立63周年,来自北京大学和清华大学的共计6名大学生志愿服务者被随机平均分配到天安门广场运送矿泉水、清扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有一名北京大学志愿者的概率是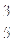 。
。
(1)求6名志愿者中来自北京大学、清华大学的各几人;
(2)求清扫卫生岗位恰好北京大学、清华大学人各一人的概率;
(3)设随机变量ζ为在维持秩序岗位服务的北京大学志愿者的人数,求ζ分布列及期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲乙两人各有一个箱子,甲的箱子里面放有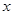 个红球,
个红球,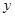 个白球(
个白球( ,且
,且 );乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.
);乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色球的个数,才能使自己获胜的概率最大?并求甲获胜的概率的最大值.
(2) 当甲获胜的概率取得最大值时,求取出的3个球中红球个数 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学生参加某高校的自主招生考试,须依次参加A、B、C、D、E五项考试,如果前四项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试。已知每一项测试都是相互独立的,该生参加A、B、C、D四项考试不合格的概率均为 ,参加第五项不合格的概率为
,参加第五项不合格的概率为
(1)求该生被录取的概率;
(2)记该生参加考试的项数为 ,求
,求 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在各交通岗遇到红灯的事件是相互独立的,并且概率都是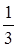 .
.
(1)求这名学生在途中遇到红灯的次数ξ的分布列;
(2)求这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的分布列;
(3)这名学生在途中至少遇到一次红灯的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com