如图，四棱锥
中，底面
是平行四边形，
，
平面
，
，
，
是
的中点.
（1）求证：
平面
；
（2）求平面
与平面
所成锐二面角的余弦值.
（1）见解析；（2）
.
【解析】
试题分析：（1）利用直线与平面垂直的性质定理以及判定定理即可证明．
， 
，所以
平面
；
（2）利用空间向量求解，平面
与平面
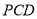所成锐二面角的余弦值即为两平面的法向量所成角或补角的余弦值．以点
为原点，
分别为
轴建立空间直角坐标系，可求平面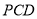
的一个法向量
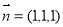；平面
的一个法向量
，所以则
.
(1)
平面
，
平面
，
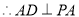
由已知条件得：，
，所以平面 （5分）
由（1）结合已知条件以点为原点，分别为轴建立空间直角坐标系，则：
，
，
，
，
，所以
7分
设
是平面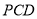的一个法向量，则
，
即：
，取
，则得：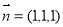
同理可求：平面的一个法向量 10分
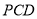设：平面和平面成角为
，
则 12分
考点：直线与平面垂直的性质定理以及判定定理、空间向量法求二面角.
科目：高中数学 来源：2015届吉林省长春市新高三起点调研考试文科数学试卷（解析版） 题型：解答题
每年5月17日为国际电信日，某市电信公司在电信日当天对办理应用套餐的客户进行优惠，优惠方案如下：选择套餐一的客户可获得优惠200元，选择套餐二的客户可获得优惠500元，选择套餐三的客户可获得优惠300元.电信日当天参与活动的人数统计结果如图所示，现将频率视为概率.
(1) 求某人获得优惠金额不低于300元的概率；
(2) 若采用分层抽样的方式从参加活动的客户中选出6人，再从该6人中随机选出两人，求这两人获得相等优惠金额的概率.
查看答案和解析>>
科目：高中数学 来源：2015届吉林省长春市高二下学期期末考试文科数学试卷（解析版） 题型：选择题
若函数
，则（ ）
A．最大值为
，最小值为
B．最大值为
，无最小值
C．最小值为
，无最大值 D．既无最大值也无最小值
查看答案和解析>>
科目：高中数学 来源：2015届吉林省长春市高二下学期期中考试理科数学试卷（解析版） 题型：选择题
在一次反恐演习中，我方三架武装直升机分别从不同方位对同一目标发动攻击（各
发射一枚导弹），由于天气原因，三枚导弹命中目标的概率分别为
，若至少有两枚导弹命中目标方可将其摧毁，则目标被摧毁的概率为（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学 来源：2014-2015学年辽宁省沈阳市高二上学期10月月考数学试卷（解析版） 题型：解答题
（本小题满分12分）若数列
满足前
项之和
且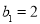
，
（1）求数列
的通项公式
（2）证明：
是等差数列
（3）求
的前
项和
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，则
（ ）
B.
C.
D.
，则
（ ）
B.
C.
D.
展开式中的常数项是 ．
，若函数
在
上有两个不同零点，则
的取值范围是( )
B.
C.
D.