
| 2 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
科目:高中数学 来源: 题型:
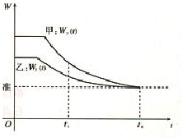 国家环保总局对长期超标准排放污物,污染严重而又未进行治理的单位,规定出一定期限,强令在此期限内完成排污治理.如图是国家环保总局在规定的排污达标日期前,对甲、乙两家企业连续检测的结果(W表示排污量),哪个企业治理的效率比较高?为什么?
国家环保总局对长期超标准排放污物,污染严重而又未进行治理的单位,规定出一定期限,强令在此期限内完成排污治理.如图是国家环保总局在规定的排污达标日期前,对甲、乙两家企业连续检测的结果(W表示排污量),哪个企业治理的效率比较高?为什么?查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| x2 |
| 1 |
| x1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com