
【题目】在平面直角坐标系xOy中,已知点A,B的坐标分别为(﹣2,0),(2,0).直线AP,BP相交于点P,且它们的斜率之积是﹣ ![]() .记点P的轨迹为Г. (Ⅰ)求Г的方程;
.记点P的轨迹为Г. (Ⅰ)求Г的方程;
(Ⅱ)已知直线AP,BP分别交直线l:x=4于点M,N,轨迹Г在点P处的切线与线段MN交于点Q,求 ![]() 的值.
的值.
【答案】解:(Ⅰ)设点P坐标为(x,y),则 直线AP的斜率 ![]() (x≠﹣2);
(x≠﹣2);
直线BP的斜率 ![]() (x≠2).
(x≠2).
由已知有 ![]() (x≠±2),
(x≠±2),
化简得点P的轨迹Г的方程为 ![]() (x≠±2).
(x≠±2).
(Ⅱ)设P(x1 , y1)(x1≠±2),则 ![]() .
.
直线AP的方程为 ![]() ,令x=4,得点M纵坐标为
,令x=4,得点M纵坐标为 ![]() ;
;
直线BP的方程为 ![]() ,令x=4,得点N纵坐标为
,令x=4,得点N纵坐标为 ![]() ;
;
设在点P处的切线方程为y﹣y1=k(x﹣x1),
由 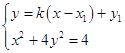 ,得
,得 ![]() .
.
由△=0,得 ![]() =0,
=0,
整理得 ![]() .
.
将 ![]() 代入上式并整理得:
代入上式并整理得: ![]() ,解得
,解得 ![]() ,
,
∴切线方程为 ![]() .
.
令x=4得,点Q纵坐标为 ![]() =
= ![]() .
.
设 ![]() ,则yQ﹣yM=λ(yN﹣yQ),
,则yQ﹣yM=λ(yN﹣yQ),
∴ 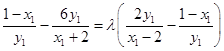 .
.
∴ 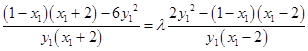 .
.
将 ![]() 代入上式,得
代入上式,得 ![]() ,
,
解得λ=1,即 ![]() =1.
=1.
【解析】(Ⅰ)设出P点坐标,求得AP、BP所在直线的斜率,由斜率之积是﹣ ![]() 列式整理即可得到Г的方程;(Ⅱ)设出P点坐标,得到AP、BP的方程,进一步求出M、N的纵坐标,再写出椭圆在P点的切线方程,由判别式等于0得到过P的斜率(用P的坐标表示),再代入切线方程,求得Q点纵坐标,设
列式整理即可得到Г的方程;(Ⅱ)设出P点坐标,得到AP、BP的方程,进一步求出M、N的纵坐标,再写出椭圆在P点的切线方程,由判别式等于0得到过P的斜率(用P的坐标表示),再代入切线方程,求得Q点纵坐标,设 ![]() ,转化为坐标的关系即可求得λ,从而得到
,转化为坐标的关系即可求得λ,从而得到 ![]() 的值.
的值.
【考点精析】关于本题考查的椭圆的标准方程,需要了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点![]() ,直线l:
,直线l:![]() ,设圆C的半径为1,圆心C在直线l上.
,设圆C的半径为1,圆心C在直线l上.
![]() 过点A作圆C的切线AP且P为切点,当切线AP最短时,求圆C的标准方程;
过点A作圆C的切线AP且P为切点,当切线AP最短时,求圆C的标准方程;
![]() 若圆C上存在点M,使
若圆C上存在点M,使![]() ,求圆心C的横坐标a的取值范围.
,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人用一网箱饲养中华鲟,研究表明:一个饲养周期,该网箱中华鲟的产量![]() (单位:百千克)与购买饲料费用
(单位:百千克)与购买饲料费用![]() (
(![]() )(单位:百元)满足:
)(单位:百元)满足:![]() .另外,饲养过程中还需投入其它费用
.另外,饲养过程中还需投入其它费用![]() .若中华鲟的市场价格为
.若中华鲟的市场价格为![]() 元/千克,全部售完后,获得利润
元/千克,全部售完后,获得利润![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,利润最大,最大利润是多少元?
为何值时,利润最大,最大利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知a1>1,an+1=an2﹣an+1(n∈N*),且 ![]()
![]() +…+
+…+ ![]() =2.则当a2016﹣4a1取得最小值时,a1的值为= .
=2.则当a2016﹣4a1取得最小值时,a1的值为= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元. (Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,n∈N)的函数解析式f(n);
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市地产数据研究所的数据显示,2016年该市新建住宅销售均价走势如图所示,3月至7月房价上涨过快,政府从8月采取宏观调控措施,10月份开始房价得到很好的抑制.

(1)地产数据研究所发现,3月至7月的各月均价![]() (万元/平方米)与月份
(万元/平方米)与月份![]() 之间具有较强的线性相关关系,试求
之间具有较强的线性相关关系,试求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若政府不调控,按照3月份至7月份房价的变化趋势预测12月份该市新建住宅的销售均价.
参考数据:![]() ,
,![]() ,
,![]() ;
;
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮胎集团有限公司生产的轮胎的宽度![]() (单位:
(单位: ![]() )服从正态分布
)服从正态分布![]() ,公司规定:轮胎宽度不在
,公司规定:轮胎宽度不在![]() 内将被退回生产部重新生产.
内将被退回生产部重新生产.
(1)求此轮胎不被退回的概率(结果精确到![]() );
);
(2)现在该公司有一批轮胎需要进行初步质检,检验方案是从这批轮胎中任取![]() 件作检验,这
件作检验,这![]() 件产品中至少有
件产品中至少有![]() 件不被退回生产部,则称这批轮胎初步质检合格.
件不被退回生产部,则称这批轮胎初步质检合格.
()求这批轮胎初步质检合格的概率;
()若质检部连续质检了![]() 批轮胎,记
批轮胎,记![]() 为这
为这![]() 批轮胎中初步质检合格的批数,求
批轮胎中初步质检合格的批数,求![]() 的数学期望.
的数学期望.
附:若![]() ,则
,则![]()
![]()
![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客的购物总额(单位元),将数据按照
位顾客的购物总额(单位元),将数据按照![]()
![]() ,
,![]()
![]() 分成
分成![]() 组,制成了如下图所示的频率分布直方图:
组,制成了如下图所示的频率分布直方图:
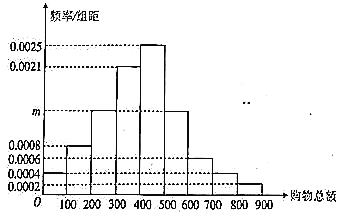
该商场每日大约有![]() 名顾客,为了增加商场销售总额,近期对一次性购物不低于
名顾客,为了增加商场销售总额,近期对一次性购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(1)求频率分布直方图中![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(2)若每日按分层抽样的方法从购物总额在![]() 三组对应的顾客中抽取
三组对应的顾客中抽取![]() 名顾客,这
名顾客,这![]() 名顾客中再随机抽取两名超级顾客,每人奖励一个超级礼包,求获得超级礼包的两人来自不同组的概率.
名顾客中再随机抽取两名超级顾客,每人奖励一个超级礼包,求获得超级礼包的两人来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调查来自南方和北方的同龄大学生的身高差异,从2016级的年龄在18~19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名,测量他们的身高,量出的身高如下(单位:cm):
南方:158,170,166,169,180,175,171,176,162,163.
北方:183,173,169,163,179,171,157,175,184,166.
(1)根据抽测结果,画出茎叶图,对来自南方和北方的大学生的身高作比较,写出统计结论.
(2)设抽测的10名南方大学生的平均身高为![]() cm,将10名南方大学生的身高依次输入如图所示的程序框图进行运算,问输出的s大小为多少?并说明s的统计学意义。
cm,将10名南方大学生的身高依次输入如图所示的程序框图进行运算,问输出的s大小为多少?并说明s的统计学意义。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com