
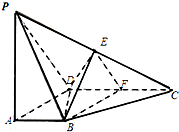
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB=2,E,F分别为PC,CD的中点.分析 (Ⅰ)只需证明AB⊥BF.AB⊥EF即可.
(Ⅱ)以A为原点,以AB,AD,AP为x轴,y轴,z轴正向建立空间直角坐标系,
求出平面CDB的法向量为$\overrightarrow{{n}_{1}}=\{0,0,1)$,平面EDB的法向量为$\overrightarrow{{n}_{2}}=(x,y,z)$,
设二面角E-BD-C的大小为θ,则$cosθ=|cos<\overrightarrow{n_1},\overrightarrow{n_2}>|=\frac{{|\overrightarrow{n_1}•\overrightarrow{n_2}|}}{{|{{\overrightarrow n}_1}|•|\overrightarrow{n_2}|}}$=$\frac{{\sqrt{5}}}{{1×\sqrt{10}}}=\frac{{\sqrt{2}}}{2}$,
解答 解:(Ⅰ)证:由已知DF∥AB且∠DAB为直角,故ABFD是矩形,
从而AB⊥BF.
又PA⊥底面ABCD,∴平面PAD⊥平面ABCD,
∵AB⊥AD,故AB⊥平面PAD,∴AB⊥PD,
在△PCD内,E、F分别是PC、CD的中点,EF∥PD,∴AB⊥EF.
由此得AB⊥平面BEF…(6分)
(Ⅱ)以A为原点,以AB,AD,AP为x轴,y轴,z轴正向建立空间直角坐标系,
则$\overrightarrow{BD}=(-1,2,0),\overrightarrow{BE}=(0,1,\frac{\sqrt{5}}{5})$
设平面CDB的法向量为$\overrightarrow{{n}_{1}}=\{0,0,1)$,平面EDB的法向量为$\overrightarrow{{n}_{2}}=(x,y,z)$,
则 $\left\{{\begin{array}{l}{\overrightarrow{n_2}•\overrightarrow{BD}=0}\\{\overrightarrow{n_2}•\overrightarrow{BE}=0}\end{array}}\right.$$\left\{\begin{array}{l}-x+2y=0\\ y+\frac{{\sqrt{5}z}}{5}=0\end{array}\right.$可取$\overrightarrow{n_2}=({2,1,-\sqrt{5}})$
设二面角E-BD-C的大小为θ,则$cosθ=|cos<\overrightarrow{n_1},\overrightarrow{n_2}>|=\frac{{|\overrightarrow{n_1}•\overrightarrow{n_2}|}}{{|{{\overrightarrow n}_1}|•|\overrightarrow{n_2}|}}$=$\frac{{\sqrt{5}}}{{1×\sqrt{10}}}=\frac{{\sqrt{2}}}{2}$,
所以,$θ=\frac{π}{4}$…(12分)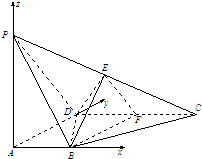
点评 本题考查了空间线面垂直的判定,向量法求二面角,属于中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(理)试卷(解析版) 题型:选择题
已知等差数列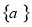 ,
, 为数列
为数列 的前
的前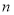 项和,若
项和,若 (
( ),记数列
),记数列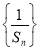 的前
的前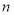 项和为
项和为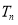 ,则
,则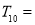 ( )
( )
A.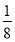 B.
B.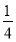
C. D.
D.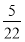
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳县四中高三9月月考数学(文)试卷(解析版) 题型:选择题
具有性质: 的函数,我们称为满足“倒负”变换的函数,下列函数:
的函数,我们称为满足“倒负”变换的函数,下列函数:
①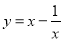 ;②
;② ;③
;③ 其中满足“倒负”变换的函数是( )
其中满足“倒负”变换的函数是( )
A.①② B.①③ C.②③ D.①
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱椎P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD为梯形,AB∥CD,∠BAD=∠ADC=90°,DC=2AB=2,DA=PD=$\sqrt{3}$,E为BC的中点,连结AE,交BD于点O.
如图,在四棱椎P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD为梯形,AB∥CD,∠BAD=∠ADC=90°,DC=2AB=2,DA=PD=$\sqrt{3}$,E为BC的中点,连结AE,交BD于点O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=g(x)的最小正周期为π | |
| B. | 函数y=g(x)的图象的一条对称轴为直线x=$\frac{π}{8}$ | |
| C. | ${∫}_{0}^{\frac{π}{2}}$g(x)dx=$\sqrt{2}$ | |
| D. | 函数y=g(x)在区间[$\frac{π}{12}$,$\frac{5π}{8}$]上单调递减 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com