
分析 设z=x+yi (x、y∈R),然后代入z2+2|$\overline{z}$|=3进行化简变形,再根据复数相等的定义建立等式关系,解之即可求出复数z.
解答 解:设z=x+yi (x、y∈R),
则原方程变成x2-y2+2xyi+2$\sqrt{{x}^{2}+{y}^{2}}$-3=0.
?$\left\{\begin{array}{l}{{x}^{2}-{y}^{2}+2\sqrt{{x}^{2}+{y}^{2}}-3=0}\\{2xy=0}\end{array}\right.$?$\left\{\begin{array}{l}{x=0}\\{-{y}^{2}+2|y|-3=0}\end{array}\right.$或$\left\{\begin{array}{l}{y=0}\\{{x}^{2}+2|x|-3=0}\end{array}\right.$(4分)
?$\left\{\begin{array}{l}{y=0}\\{x=1}\end{array}\right.$
∴z为1.
点评 本题主要考查了复数的模,以及复数相等的重要条件,同时考查了计算能力,属于基础题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 最大值为1,图象关于直线x=$\frac{π}{2}$对称 | B. | 在(0,$\frac{π}{4}$)上单调递减,为奇函数 | ||
| C. | 在(-$\frac{3π}{8}$,$\frac{π}{8}$)上单调递增,为偶函数 | D. | 周期为π,图象关于点($\frac{3π}{8}$,0)对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
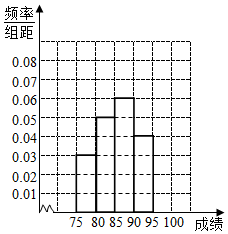 将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分.
将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com