
已知函数f(x)=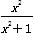 ,则f(1)+f(2)+…+f(2 013)+f(2 014)+
,则f(1)+f(2)+…+f(2 013)+f(2 014)+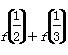 +…+
+…+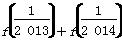 =( )
=( )
A.2 010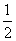 B.2 011
B.2 011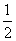
C.2 012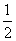 D.2 013
D.2 013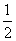
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
已知集合A={x êx2+(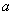 -1)x-
-1)x-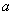 >0},B={x ê(x+
>0},B={x ê(x+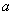 )(x+b)>0},其中
)(x+b)>0},其中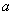 ≠b,M={x êx2-2x-3≤0},全集I=R.
≠b,M={x êx2-2x-3≤0},全集I=R.
(1)若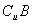 =M,求a、b的值;
=M,求a、b的值;
(2)若a>b>-1,求A∩B;
(3)若a2+ ∈
∈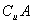 ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}是等差数列,{bn}是等比数列,其中a1=b1=1,a2≠b2,且b2为a1,a2的等差中项,a2为b2,b3的等差中项.
(1)求数列{an}与{bn}的通项公式;
(2)记cn=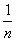 (a1+a2+…+an)(b1+b2+…+bn),求数列{cn}的前n项和Sn.
(a1+a2+…+an)(b1+b2+…+bn),求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知定义在R上的函数f(x)是奇函数且满足f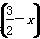 =f(x),f(-2)=5,数列{an}满足a1=-1,且
=f(x),f(-2)=5,数列{an}满足a1=-1,且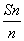 =2×
=2×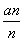 +1(其中Sn为{an}的前n项和),则f(a6)+f(a7)=________.
+1(其中Sn为{an}的前n项和),则f(a6)+f(a7)=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x+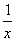 (x>0),以点(n,f(n))为切点作函数图象的切线ln(n∈N*),直线x=n+1与函数y=f(x)图象及切线ln分别相交于An,Bn,记an=|AnBn|.
(x>0),以点(n,f(n))为切点作函数图象的切线ln(n∈N*),直线x=n+1与函数y=f(x)图象及切线ln分别相交于An,Bn,记an=|AnBn|.
(1)求切线ln的方程及数列{an}的通项;
(2)设数列{nan}的前n项和为Sn,求证:Sn<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)的定义域为D,若f(x)满足下面两个条件则称f(x)为闭函数:①f(x)是D上的单调函数;②存在[a,b]⊆D,使f(x)在[a,b]上的值域为[a,b].现已知f(x)=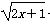 +k为闭函数,则k的取值范围是( )
+k为闭函数,则k的取值范围是( )
A.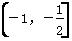 B.(-∞,1)
B.(-∞,1)
C.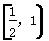 D.(-1,+∞)
D.(-1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com