
分析 作出图象,由向量的运算法则易得答案,其中$\overrightarrow{ON}$=$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$)是解决问题的关键.
解答 解: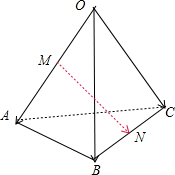 如图结合向量的运算法则可得:
如图结合向量的运算法则可得:
$\overrightarrow{MN}$=$\overrightarrow{ON}$-$\overrightarrow{OM}$=
$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$)-$\frac{1}{2}$$\overrightarrow{OA}$
=$\frac{1}{2}$($\overrightarrow b$+$\overrightarrow c$)-$\frac{1}{2}$$\overrightarrow a$
=$-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$,
故答案为:$-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$
点评 本题考查向量的加减混合运算及几何意义,向量在几何中的应用,难度基础.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=sin({2x-\frac{π}{4}})+1$ | B. | y=2cos2x | C. | y=2sin2x | D. | y=cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “x≠1”是“x2≠1”的充分不必要条件 | |
| B. | 若“p∧q”与“?p∨q”都是假命题,则p真q假 | |
| C. | 命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x<0” | |
| D. | 命题“能被2整除的数是偶数”的逆否命题是“不能被2整除的数不是偶数” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com