练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某公司生产一种电子仪器的固定成本为20 000元，每生产一台仪器需增加投入100元，已知总收益满足函数：

    R(x)＝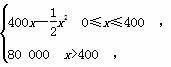

    其中x是仪器的月产量．

    (1)将利润表示为月产量的函数f(x)；

    (2)当月产量为何值时，公司所获利润最大？最大利润为多少元？(总收益＝总成本＋利润)


    解析：　(1)设月产量为x台，则总成本为20 000＋100x，从而f(x)＝

    (2)当0≤x≤400时，

    f(x)＝－(x－300)2＋25 000.

    ∴当x＝300时，有最大值为25 000；

    当x>400时，

    f(x)＝60 000－100x是减函数，

    f(x)<60 000－100×400＝20 000<25 000.

    ∴当x＝300时，f(x)的最大值为25 000，

    即每月生产300台仪器时，利润最大，最大利润为25 000元．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设集合A是由1，－2，a2－1三个元素构成的集合，集合B是由1，a2－3a，0三个元素构成的集合，若A＝B，则实数a＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    计算下列各式的值：

     ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    化简(2a－3b－)·(－3a－1b)÷(4a－4b－)得________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知A，B两地相距150千米，某人开汽车以60千米/时的速度从A地到达B地，在B地停留1小时后再以50千米/时的速度返回A地，则汽车离开A地的距离x关于时间t(小时)的函数解析式是(　　)

    A．x＝60t

    B．x＝60t＋50t

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若x∈(0,1)，则下列结论正确的是(　　)

    A．2x>x>lg x                       B．2x>lg x>x

    C．x>2x>lg x                       D．lg x>x>2x

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若函数f(x)唯一的一个零点同时在区间(0,16)，(0,8)，(0,4)，(0,2)内，那么下列说法中正确的是(　　)

    A．函数f(x)在区间(0,1)内有零点

    B．函数f(x)在区间(0,1)或(1,2)内有零点

    C．函数f(x)在区间(2,16)内无零点

    D．函数f(x)在区间(1,16)内无零点

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知二次函数f(x)＝x2－2ax＋4，求在下列条件下，实数a的取值范围．

    (1)零点均大于1；

    (2)一个零点大于1，一个零点小于1；

    (3)一个零点在(0,1)内，另一个零点在(6,8)内．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    阅读下面语句：

    语句计算结果为________．

    查看答案和解析>>

    同步练习册答案