
| A. | 60条 | B. | 66条 | C. | 72条 | D. | 78条 |
分析 直线是截距式方程,因而不平行坐标轴,不过原点,考查圆上横坐标和纵坐标均为整数的点的个数,结合排列组合知识分类解答.
解答 解:可知直线的横、纵截距都不为零,即与坐标轴不垂直,不过坐标原点,而圆x2+y2=169上的整数点共有12个,分别为(5,±12),(-5,±12),(12,±5),(-12,±5),(±13,0),(0,±13),
前8个点中,过任意一点的圆的切线满足,有8条;
12个点中过任意两点,构成C122=66条直线,其中有4条直线垂直x轴,有4条直线垂直y轴,还有6条过原点(圆上点的对称性),
故满足题设的直线有52条.
综上可知满足题设的直线共有52+8=60条,
故选:A.
点评 此题考查了直线与圆相交的性质,是以直线和圆为载体,考查数学的综合应用能力.学生做题时一定要注意与y轴平行的直线斜率不存在不满足题意,要舍去.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{7}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
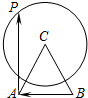 如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].
如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a} | B. | {a,b,c,d } | C. | {b,c,d } | D. | {a,e } |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com