
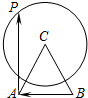
 如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].
如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4]. 分析 首先建立平面直角坐标系:以C为原点,平行于AB的直线为x轴,这样便可建立坐标系,然后便可根据条件确定出A,B点的坐标,并根据题意设P(3cosθ,3sinθ),从而可求出$\overrightarrow{BA},\overrightarrow{AP}$的坐标,进行数量积的坐标运算便得出$\overrightarrow{BA}•\overrightarrow{AP}=-12cosθ-8$,这样根据-1≤cosθ≤1便可求出$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围.
解答 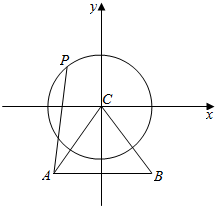 解:如图,以C为坐标原点,以平行于AB的直线为x轴,垂直于AB的直线为y轴,建立平面直角坐标系,则:
解:如图,以C为坐标原点,以平行于AB的直线为x轴,垂直于AB的直线为y轴,建立平面直角坐标系,则:
$A(-2,-2\sqrt{3}),B(2,-2\sqrt{3})$;
点P是以点C为圆心、3为半径的圆上的任意一点;
∴设P(3cosθ,3sinθ);
∴$\overrightarrow{BA}=(-4,0),\overrightarrow{AP}=(3cosθ+2,3sinθ+2\sqrt{3})$;
∴$\overrightarrow{BA}•\overrightarrow{AP}=-12cosθ-8$;
∵-1≤cosθ≤1;
∴-20≤-12cosθ-8≤4;
∴$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围为[-20,4].
故答案为:[-20,4].
点评 考查通过建立平面直角坐标系,利用向量的坐标解决向量问题的方法,能求平面上点的坐标,根据坐标可以求向量的坐标,用三角函数表示圆上的点的坐标的方法,以及向量数量积的坐标运算,余弦函数的值域.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60条 | B. | 66条 | C. | 72条 | D. | 78条 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
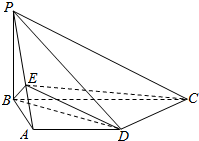 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com