
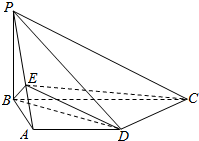
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.分析 (1)连结AC交BD于F,连结EF,由线面平行的性质得PC∥EF,故而$\frac{PE}{EA}=\frac{FC}{FA}$,由于底面为直角梯形,AB=AD,BD⊥CD可得△BCD是等腰直角三角形,从而求出BC,于是$\frac{FC}{FA}=\frac{BC}{AD}$;
(2)求出E到底面的距离和△BCD的面积即可求出棱锥的体积.
解答 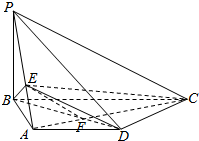 解:(1)连结AC交BD于F,连结EF,
解:(1)连结AC交BD于F,连结EF,
∵PC∥平面BDE,PC?平面APC,平面APC∩平面BDE=EF,
∴PC∥EF,∴$\frac{PE}{EA}=\frac{FC}{FA}$.
∵四边形ABCD是直角梯形,AD∥BC,CD⊥BD,
∴AB⊥AD,AB⊥BC,
∵AB=AD=3,∴BD=3$\sqrt{2}$,∠ABD=∠ADB=45°,
∴∠DBC=45°,又∵BD⊥CD,
∴△BCD是等腰直角三角形,∴BC=$\sqrt{2}$BD=6.
∵AD∥BC,∴△ADF∽△CFB,
∴$\frac{FC}{FA}=\frac{BC}{AD}$=$\frac{6}{3}$=2.
∴λ=2.
(2)∵$\frac{PE}{EA}=2$,PB⊥平面ABCD,
∴E到底面ABCD的距离h=$\frac{1}{3}$PB=1.
∴三棱锥B-EDC的体积V=V棱锥E-BCD=$\frac{1}{3}$×$\frac{1}{2}$×BD×CD×h=$\frac{1}{3}×\frac{1}{2}×3\sqrt{2}×3\sqrt{2}×1$=3.
点评 本题考查了线面平行的性质,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | p∨(¬q) | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2=-4y | B. | x2=12y | C. | x2=-4y或x2=12y | D. | 以上都不是 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
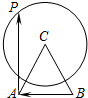 如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].
如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x/百万元 | 2 | 4 | 5 | 6 | 8 |
| y/百万元 | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com