
| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
分析 ①x2-y2=1 是一个等轴双曲线,没有自公切线;
②在x=$\frac{1}{2}$和x=-$\frac{1}{2}$处的切线都是y=-$\frac{1}{4}$,故②有自公切线;
③此函数是周期函数,过图象的最高点的切线都重合或过图象的最低点的切线都重合,此函数有自公切线;
④结合图象可得,此曲线没有自公切线.
解答 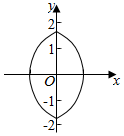 解:①x2-y2=1 是一个等轴双曲线,没有自公切线;
解:①x2-y2=1 是一个等轴双曲线,没有自公切线;
②y=x2-|x|=$\left\{\begin{array}{l}{(x-\frac{1}{2})^{2}-\frac{1}{4},x≥0}\\{(x+\frac{1}{2})^{2}-\frac{1}{4},x<0}\end{array}\right.$,
在x=$\frac{1}{2}$和x=-$\frac{1}{2}$处的切线都是y=-$\frac{1}{4}$,故②有自公切线;
③y=3sinx+4cosx=5sin(x+φ),cosφ=$\frac{3}{5}$,sinφ=$\frac{4}{5}$,此函数是周期函数,
过图象的最高点的切线都重合或过图象的最低点的切线都重合,故此函数有自公切线;
④由于|x|+1=$\sqrt{4-{y}^{2}}$,即x2+2|x|+y2-3=0,图象如右,结合图象可得,此曲线没有自公切线.
故选:D.
点评 正确理解新定义“自公切线”,正确画出函数的图象、数形结合的思想方法是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
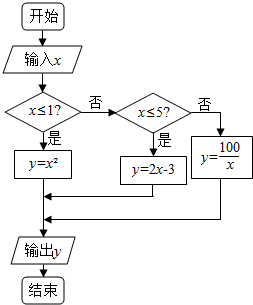 如图,给出了一个程序框图,其作用是输入x的值,输出相应y的值.
如图,给出了一个程序框图,其作用是输入x的值,输出相应y的值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
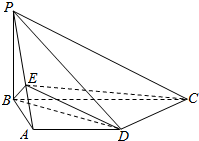 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,CD⊥BD,PB⊥平面ABCD,PB=AB=AD=3,点E在线段PA上,且满足$\frac{PE}{EA}$=λ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={({\frac{1}{2}})^x}$ | B. | $y={2^{{{log}_2}x}}$ | C. | y=2x | D. | $y={log_2}{2^{-x}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com