
分析 求导f′(x)=ex-2,从而可得f(x)的单调性,从而由单调性确定函数的极值即可.
解答 解:∵f(x)=ex-2x+a,
∴f′(x)=ex-2,
∴当x∈(-∞,ln2)时,f′(x)<0,
故f(x)在(-∞,ln2)上单调递减,
当x∈(ln2,+∞)时,f′(x)>0,
故f(x)在(ln2,+∞)上单调递增,
而f(0)=1+a,f(ln2)=2-2ln2+a,$\underset{lim}{x→+∞}$f(x)=+∞;
故2-2ln2+a<0<1+a,
故a∈(-1,2ln2-2).
故答案为:(-1,2ln2-2).
点评 本题考查了导数的综合应用及分类讨论的思想应用,同时考查了方程的根与函数的零点的关系应用.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2=-4y | B. | x2=12y | C. | x2=-4y或x2=12y | D. | 以上都不是 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{7}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
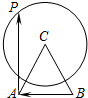 如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].
如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com