
分析 (Ⅰ)当a=2时,函数f(x)=|x-2|,不等式$\frac{f(x-2)-f(x+1)}{f(x-1)-f(x)}$<$\frac{f(x-1)+f(x)}{f(x-2)}$可化为:$\frac{|x-4|-|x-1|}{|x-3|-|x-2|}<\frac{|x-3|+|x-2|}{|x-4|}$,利用零点分段法,可得不等式的解集;
(Ⅱ)若关于x的不等式|f(2x+a)-2f(x)|≤2的解集为{x|1≤x≤2},则1,2为方程|f(2x+a)-2f(x)|=2的两根,求出相应的a值后,检验可得答案.
解答 解:(Ⅰ)当a=2时,函数f(x)=|x-2|,
不等式$\frac{f(x-2)-f(x+1)}{f(x-1)-f(x)}$<$\frac{f(x-1)+f(x)}{f(x-2)}$可化为:$\frac{|x-4|-|x-1|}{|x-3|-|x-2|}<\frac{|x-3|+|x-2|}{|x-4|}$,
当x=$\frac{5}{2}$或x=4时,原不等式无意义,
(1)当x≤1时,不等式可化为:$\frac{-(x-4)+(x-1)}{-(x-3)+(x-2)}<\frac{-(x-3)-(x-2)}{-(x-4)}$,即$3<\frac{-2x+5}{-x+4}$,即-3x+12<-2x+5,解得:x>7,此时原不等式无解;
(2)当1<x≤2时,不等式可化为:$\frac{-(x-4)-(x-1)}{-(x-3)+(x-2)}<\frac{-(x-3)-(x-2)}{-(x-4)}$,即-2x+5$<\frac{-2x+5}{-x+4}$,即2x2-11x+15<0,解得:$\frac{5}{2}<x<3$,此时原不等式无解;
(3)当2<x<3且x≠$\frac{5}{2}$时,不等式可化为:$\frac{-(x-4)-(x-1)}{-(x-3)-(x-2)}<\frac{-(x-3)+(x-2)}{-(x-4)}$,即4-x<1,解得:x>3此时原不等式无解;
(4)当3≤x<4时,不等式可化为:$\frac{-(x-4)-(x-1)}{(x-3)-(x-2)}<\frac{(x-3)+(x-2)}{-(x-4)}$,即(2x-5)(x-3)>0,解得:x>3,或x<$\frac{5}{2}$,故3<x<4,
(5)当x>4时,不等式可化为:$\frac{(x-4)-(x-1)}{(x-3)-(x-2)}<\frac{(x-3)+(x-2)}{x-4}$,即3x-12<2x-5,解得:x<7,故4<x<7,
综上可得:不等式$\frac{f(x-2)-f(x+1)}{f(x-1)-f(x)}$<$\frac{f(x-1)+f(x)}{f(x-2)}$的解集为(3,4)∪(4,7);
(Ⅱ)若关于x的不等式|f(2x+a)-2f(x)|≤2的解集为{x|1≤x≤2},
则1,2为方程|f(2x+a)-2f(x)|=2的两根,
即1,2为方程||2x|-2|x-a||=2的两根,
即$\left\{\begin{array}{l}|2-2|1-a\left|\right|=2\\|4-2|2-a\left|\right|=2\end{array}\right.$
解得:a=1,a=-1,或a=3,
经检验当a=3时,不满足条件,
故a=±1
点评 本题考查的知识点是绝对值不等式的解法,零点分段法,分类讨论思想,不等式解集与相应方程根的关系,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 2x+y+2=0 | B. | 2x+y+3=0 | C. | 2x-y-1=0 | D. | 2x-y+1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 0 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
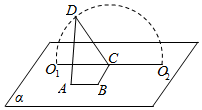 如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com