
分析 解不等式求出M,N,根据M∪N=M,可得N⊆M,分三种情况分别求出满足条件的实数a的取值范围,综合讨论结果,可得答案.
解答 解:∵集合M={x|x2-3x≤10}={x|x2-3x-10≤0}=[-2,5],
N={x|x2-(3a+2)x+2a2+3a+1<0}={x|[x-(2a+1)][x-(a+1)]<0},
∵M∪N=M,
∴N⊆M,
当a>0时,N=(a+1,2a+1),
∴$\left\{\begin{array}{l}{a+1≥-2}\\{2a+1≤5}\end{array}\right.$,
解得0<a≤2,
当a=0时,N=∅,满足条件,
当a<0时,N=(2a+1,a+1),
∴$\left\{\begin{array}{l}{2a+1≥-2}\\{a+1≤5}\end{array}\right.$,
解得-$\frac{3}{2}$≤a<0,
综上满足条件的实数a的取值范围是[-$\frac{3}{2}$,2]
故答案为:[-$\frac{3}{2}$,2]
点评 本题考查的知识点是集合的并集及基运算,其中将M∪N=M转化为N⊆M是解答的关键.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨q | C. | p∨(¬q) | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-$\sqrt{2}$ | B. | -1+$\sqrt{2}$ | C. | 1+$\sqrt{2}$ | D. | 1-$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
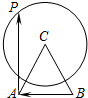 如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].
如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com