
已知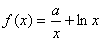 ,
, 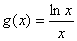 ,
,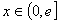 ,其中
,其中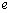 是无理数且
是无理数且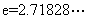 ,
,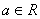 .
.
(1)若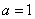 ,求
,求 的单调区间与极值;
的单调区间与极值;
(2)求证:在(1)的条件下,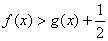 ;
;
(3)是否存在实数 ,使
,使 的最小值是
的最小值是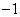 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
椭圆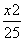 +
+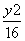 =1的左、右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|值为___
=1的左、右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|值为___
查看答案和解析>>
科目:高中数学 来源: 题型:
f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)—f(x)≤0,对任意正数a,b,若a<b,则必有( )
A.af(b)≤bf(a) B.bf(a)≤af(b) C.af(a)≤f(b) D.bf(b)≤f(a)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合P={3,log2a},Q={a,b},若P∩Q={0},则P∪Q等于( )
A.{3,0} B.{3,0,1}
C.{3,0,2} D.{3,0,1,2}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com