考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:(1)由题意知AA
1,AB,AC两两垂直,建立空间直角坐标系,求出平面A
1CC
1的法向量,进而根据BE的方向向量与平面A
1CC
1的法向量平行,得到答案.
(2)平面C
1A
1C的法向量为
=(1,-1,1)而平面A
1CA的一个法向量为
=(1,0,0),代入向量夹角公式,可得答案.
解答:

解:(1)由题意知AA
1,AB,AC两两垂直,建立如图所示的空间直角坐标系,
则A(0,0,0),A
1(0,0,2),B(-2,0,0),C(0,-2,0),C
1(-1,-1,2),
则
=(-1,1,2),
=(-1,-1,0),
=(0,-2,-2).(1分)
设E(x,y,z),则
=(x,y+2,z),
=(-1-x,-1-y,2-z).(3分)
∵|CE|=2|EC
1|
∴
=2
,得E(
-,-
,
)
∴
=(
,-
,
),
设平面C
1A
1C的法向量为
=(x,y,z),则由
,
得
,
取x=1,则y=-1,z=1.故
=(1,-1,1),
∵
=
,
∴BE⊥平面A
1CC
1.(6分)
(2)由(1)知,平面C
1A
1C的法向量为
=(1,-1,1)而平面A
1CA的一个法向量为
=(1,0,0),
则cos<
,
>=
=
=
,故二面角C
1-A
1C-A的余弦值
-.(12分)
点评:本题考查的知识点三视图,线面垂直及二面角,其中建立空间坐标系,将空间线面关系及夹角问题转化为向量问题是解答的关键.

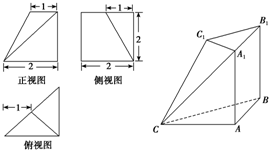
 解:(1)由题意知AA1,AB,AC两两垂直,建立如图所示的空间直角坐标系,
解:(1)由题意知AA1,AB,AC两两垂直,建立如图所示的空间直角坐标系,

 期末集结号系列答案
期末集结号系列答案