
【题目】中国海军,正在以不可阻挡的气魄向深蓝进军。在中国海军加快建设的大背景下,国产水面舰艇吨位不断增大、技术日益现代化,特别是国产航空母舰下水,航母需要大量高素质航母舰载机飞行员。为此中国海军在全国9省9所优质普通高中进行海航班建设试点培育航母舰载机飞行员。2017年4月我省首届海军航空实验班开始面向全省遴选学员,有10000名初中毕业生踊跃报名投身国防,经过文化考试、体格测试、政治考核、心理选拔等过程筛选,最终招收50名学员。培养学校在关注学员的文化素养同时注重学员的身体素质,要求每月至少参加一次野营拉练活动(下面简称“活动”)并记录成绩.10月某次活动中海航班学员成绩统计如图所示:
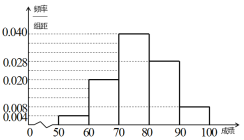
(Ⅰ)根据图表,试估算学员在活动中取得成绩的中位数(精确到![]() );
);
(Ⅱ)根据成绩从![]() 、
、![]() 两组学员中任意选出两人为一组,若选出成绩分差大于
两组学员中任意选出两人为一组,若选出成绩分差大于![]() ,则称该组为“帮扶组”,试求选出两人为“帮扶组”的概率.
,则称该组为“帮扶组”,试求选出两人为“帮扶组”的概率.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】从某企业生产的产品的生产线上随机抽取 件产品,测量这批产品的一项质量指标值,由测量结果得如图所示的频率分布直方图:
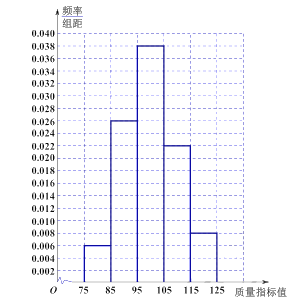
(Ⅰ) 估计这批产品质量指标值的样本平均数![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ) 若该种产品的等级及相应等级产品的利润(每件)参照以下规则(其中![]() 为产品质量指标值):
为产品质量指标值):
当![]() , 该产品定为一等品,企业可获利 200 元;
, 该产品定为一等品,企业可获利 200 元;
当![]() 且
且![]() ,该产品定为二等品,企业可获利 100 元;
,该产品定为二等品,企业可获利 100 元;
当![]() 且
且![]() ,该产品定为三等品,企业将损失 500 元;
,该产品定为三等品,企业将损失 500 元;
否则该产品定为不合格品,企业将损失 1000 元.
(ⅰ)若测得一箱产品(5 件)的质量指标数据分别为:76、85、93、105、112,求该箱产品的利润;
(ⅱ)设事件![]() ;事件
;事件![]() ;事件
;事件![]() . 根据经验,对于该生产线上的产品,事件
. 根据经验,对于该生产线上的产品,事件![]() 发生的概率分别为0.6826、0.9544、0.9974.根据以上信息,若产品预计年产量为10000件,试估计该产品年获利情况.(参考数据:
发生的概率分别为0.6826、0.9544、0.9974.根据以上信息,若产品预计年产量为10000件,试估计该产品年获利情况.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年元旦假期,高三的8名同学准备拼车去旅游,其中![]() 班、
班、![]() 班,
班,![]() 班、
班、![]() 班每班各两名,分乘甲乙两辆汽车,每车限坐4名同学
班每班各两名,分乘甲乙两辆汽车,每车限坐4名同学![]() 乘同一辆车的4名同学不考虑位置
乘同一辆车的4名同学不考虑位置![]() ,其中
,其中![]() 班两位同学是孪生姐妹,需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自同一个班的乘坐方式共有
班两位同学是孪生姐妹,需乘同一辆车,则乘坐甲车的4名同学中恰有2名同学是来自同一个班的乘坐方式共有![]()
![]()
A. 18种 B. 24种 C. 48种 D. 36种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系中,角![]() 的始边与
的始边与![]() 轴重合,终边与单位圆相交于点
轴重合,终边与单位圆相交于点![]() ,若
,若![]() 在第一象限,且
在第一象限,且![]()
(1)求点![]() 的坐标
的坐标
(2)将![]() 的终边逆时针旋转
的终边逆时针旋转![]() 大小的角后与单位圆相交于点
大小的角后与单位圆相交于点![]() ,求点
,求点![]() 的坐标
的坐标
(3)设![]() ,线段
,线段![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 角至线段
角至线段![]() ,请用
,请用![]() 表示点
表示点![]() 的坐标
的坐标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为![]() ,中奖可以获得2分:方案乙的中奖率为
,中奖可以获得2分:方案乙的中奖率为![]() ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为![]() ,求
,求![]() 的概率;
的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的均值较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某协会对![]() ,
,![]() 两家服务机构进行满意度调查,在
两家服务机构进行满意度调查,在![]() ,
,![]() 两家服务机构提供过服务的市民中随机抽取了
两家服务机构提供过服务的市民中随机抽取了![]() 人,每人分别对这两家服务机构进行独立评分,满分均为
人,每人分别对这两家服务机构进行独立评分,满分均为![]() 分.整理评分数据,将分数以
分.整理评分数据,将分数以![]() 为组距分成
为组距分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到
,得到![]() 服务机构分数的频数分布表,
服务机构分数的频数分布表,![]() 服务机构分数的频率分布直方图:
服务机构分数的频率分布直方图:


定义市民对服务机构评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 | 0 | 1 | 2 |
(1)在抽样的![]() 人中,求对
人中,求对![]() 服务机构评价“满意度指数”为
服务机构评价“满意度指数”为![]() 的人数;
的人数;
(2)从在![]() ,
,![]() 两家服务机构都提供过服务的市民中随机抽取
两家服务机构都提供过服务的市民中随机抽取![]() 人进行调查,试估计对
人进行调查,试估计对![]() 服务机构评价的“满意度指数”比对
服务机构评价的“满意度指数”比对![]() 服务机构评价的“满意度指数”高的概率;
服务机构评价的“满意度指数”高的概率;
(3)如果从![]() ,
,![]() 服务机构中选择一家服务机构,以满意度出发,你会选择哪一家?说明理由.
服务机构中选择一家服务机构,以满意度出发,你会选择哪一家?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为( )

(A)![]() (B)-
(B)-![]() (C)
(C)![]() (D)-
(D)-![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com