

分析 (Ⅰ)由样本容量和频数频率的关系易得答案;
(Ⅱ)由题意可知,分数在[80,90)内的学生有:0.010×10×50=5人,分数在[90,100)内的学生有2人,利用条件概率公式可得结论.
解答 解:(Ⅰ)由题意可知,样本容量$n=\frac{8}{0.016×10}=50$,$y=\frac{2}{50×10}=0.004$,
x=0.100-0.004-0.010-0.016-0.040=0.030.
(Ⅱ)由题意可知,分数在[80,90)内的学生有:0.010×10×50=5人,分数在[90,100)内的学生有2人;
设A={第1次抽取的成绩低于90分},B={第2次抽取的成绩仍低于90分},
则$P(A)=\frac{5}{7}$,$P({AB})=\frac{5×4}{7×6}=\frac{10}{21}$,
∴$P({B|A})=\frac{{P({AB})}}{P(A)}=\frac{2}{3}$.
点评 本题考查求条件概率,涉及频率分布直方图,属基础题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3025 | B. | -3024 | C. | 2017 | D. | 9703 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
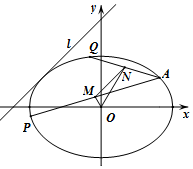 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率$e=\frac{{\sqrt{2}}}{2}$,且与直线l:y=x+3相切.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率$e=\frac{{\sqrt{2}}}{2}$,且与直线l:y=x+3相切.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x≤$\frac{1}{3}$} | B. | {x|x≥$\frac{1}{3}$} | C. | {x|x≤$\frac{1}{3}$} | D. | {x|$\frac{1}{3}$≤x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{2\sqrt{3}}{3}$) | B. | (1,2) | C. | ($\frac{2\sqrt{3}}{3}$,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
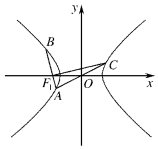 如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com